题目内容
请写出一个根为1,另一根满足-1<x<1的一元二次方程是 .
考点:根与系数的关系
专题:开放型
分析:由于另一根满足-1<x<1,则可设另一个为0,再计算1+0=1,1×0=0,然后根据根与系数的关系写出满足条件的一元二次方程.
解答:解:设另一个为0,
因为1+0=1,1×0=0,
所以以0和1为根的一元二次方程可为x2-x=0.
故答案为x2-x=0.
因为1+0=1,1×0=0,
所以以0和1为根的一元二次方程可为x2-x=0.
故答案为x2-x=0.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
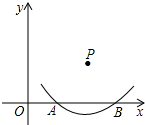 如上图,在直角坐标系中,以点P为圆心2
如上图,在直角坐标系中,以点P为圆心2| 5 |
A、(4,
| ||
| B、(4,2) | ||
| C、(4,4) | ||
D、(2,2
|
下列计算中,结果正确的是( )
| A、m8÷m2=m4 |
| B、(mn)4=mn4 |
| C、(a+b)2=a2+b2 |
| D、(a+b)(a-b)=a2-b2 |
下列各式计算正确的是( )
| A、(a-b)2=a2-b2 |
| B、a8÷a4=a2(a≠0) |
| C、2a3•3a2=6a5 |
| D、(-a2)3=a6 |
A地海拔高度是-53m,B地比A地高17m,B地的海拔高度是( )
| A、60m | B、-70m |
| C、70m | D、-36m |
下列计算中可采用平方差公式的是( )
| A、(x+y)(x-z) |
| B、(-x+2y)(x+2y) |
| C、(-3x-y)(3x+y) |
| D、(2a+3b)(2b-3a) |
关于x的方程x2+2kx-k-1=0的根的情况描述正确的是( )
| A、k为任何实数,方程都没有实数根 |
| B、k为任何实数,方程都有两个不相等的实数根 |
| C、k为任何实数,方程都有两个相等的实数根 |
| D、根据k的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 |
近似数38.57的取值范围是( )
| A、38.565≤a<38.575 |
| B、38.565<a<38.575 |
| C、38.565<a≤38.575 |
| D、38.55≤a<38.65 |