题目内容
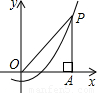
 如图,坐标系的原点为O,点P是第一象限内抛物线y=
如图,坐标系的原点为O,点P是第一象限内抛物线y= x2-1上的任意一点,PA⊥x轴于点A.则OP-PA值为
x2-1上的任意一点,PA⊥x轴于点A.则OP-PA值为
- A.1
- B.2
- C.3
- D.4
B
分析:先设P点坐标为(a, a2-1),再根据勾股定理计算出OP,然后计算OP-PA.
a2-1),再根据勾股定理计算出OP,然后计算OP-PA.
解答:设P点坐标为(a, a2-1),则OA=a,PA=
a2-1),则OA=a,PA= a2-1,
a2-1,
∴OP= =
= =
= a2+1,
a2+1,
∴OP-PA= a2+1-(
a2+1-( a2-1)=2.
a2-1)=2.
故选B.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了勾股定理.
分析:先设P点坐标为(a,
 a2-1),再根据勾股定理计算出OP,然后计算OP-PA.
a2-1),再根据勾股定理计算出OP,然后计算OP-PA.解答:设P点坐标为(a,
 a2-1),则OA=a,PA=
a2-1),则OA=a,PA= a2-1,
a2-1,∴OP=
 =
= =
= a2+1,
a2+1,∴OP-PA=
 a2+1-(
a2+1-( a2-1)=2.
a2-1)=2.故选B.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了勾股定理.

练习册系列答案
相关题目
 如图,坐标系的原点为O,点P是第一象限内抛物线
如图,坐标系的原点为O,点P是第一象限内抛物线 (2013•盐城模拟)如图,坐标系的原点为O,点P是第一象限内抛物线y=
(2013•盐城模拟)如图,坐标系的原点为O,点P是第一象限内抛物线y=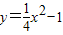 上的任意一点,PA⊥x轴于点A.则OP-PA= .
上的任意一点,PA⊥x轴于点A.则OP-PA= .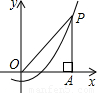
 上的任意一点,PA⊥x轴于点A.则OP-PA= .
上的任意一点,PA⊥x轴于点A.则OP-PA= .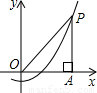
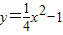 上的任意一点,PA⊥x轴于点A.则OP-PA= .
上的任意一点,PA⊥x轴于点A.则OP-PA= .