题目内容
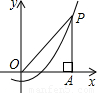
 如图,坐标系的原点为O,点P是第一象限内抛物线y=
如图,坐标系的原点为O,点P是第一象限内抛物线y=| 1 | 4 |
分析:由点P是第一象限内抛物线y=
x2-1上的任意一点,PA⊥x轴于点A,表示出P点的坐标为(x,
x2-1),进而表示出PO,PA的长,从而求出OP-PA的值.
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:∵点P是第一象限内抛物线y=
x2-1上的任意一点,PA⊥x轴于点A,
∴表示出P点的坐标为:(x,
x2-1),
∴PA=
x2-1,OA=x,
∴PO=
=
=
x2+1,
∴OP-PA=
x2+1-(
x2-1)=2.
故答案为:2.
| 1 |
| 4 |
∴表示出P点的坐标为:(x,
| 1 |
| 4 |
∴PA=
| 1 |
| 4 |
∴PO=
| PA2+OA2 |
(
|
| 1 |
| 4 |
∴OP-PA=
| 1 |
| 4 |
| 1 |
| 4 |
故答案为:2.
点评:此题主要考查了二次函数图象上点的坐标的性质,用x表示出PO,PA,OA的长度,是解决问题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 (2013•盐城模拟)如图,坐标系的原点为O,点P是第一象限内抛物线y=
(2013•盐城模拟)如图,坐标系的原点为O,点P是第一象限内抛物线y=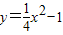 上的任意一点,PA⊥x轴于点A.则OP-PA= .
上的任意一点,PA⊥x轴于点A.则OP-PA= .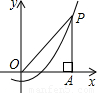
 上的任意一点,PA⊥x轴于点A.则OP-PA= .
上的任意一点,PA⊥x轴于点A.则OP-PA= .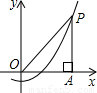
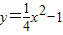 上的任意一点,PA⊥x轴于点A.则OP-PA= .
上的任意一点,PA⊥x轴于点A.则OP-PA= .