Question

【题目】在平面直角坐标系中，点的坐标为，点的变换点的坐标定义如下：当时，点的坐标为；当时，点的坐标为．

（1）点的变换点的坐标是_________；点的变换点为，连接，，则__________；

（2）若点是函数图象上的一点，点的变换点为，连接，求线段长的取值范围；

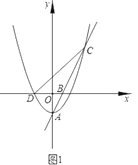
（3）已知抛物线与轴交于点，（点在点的左侧），顶点为．点在抛物线上，点的变换点为．若点恰好在抛物线的对称轴上，且四边形是菱形，求的值．

Answer 1

【答案】（1）（-3，1）；90；（2）；（3）m=8或m=2或m=3．

【解析】

（1）、根据对应的定义可以直接求得的坐标，然后依据题意画出图形，过点B作BC⊥y轴，垂足为C，过点作D⊥y轴，垂足为D，然后证明≌（SAS），由全等三角形的性质得到，然后可求得；

（2）、设点F的坐标为（x，-2x-6），依题意可得，然后依据两点间距离公式得到的长度与x的函数关系式，从而求到的取值范围；

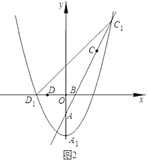
（3）、抛物线的顶点E的坐标为E（-2，m），m＞0，设点P的坐标为，①若，则点，然后依据点恰好在抛物线的对称轴上，且四边形是菱形，可得到关于m和x的方程组，从而求到m的值；②若，则点，同理得到关于m和x的方程组，从而求到m的值．

解：（1）∵点A（3，1），3＞1，

∴点A的对应点的坐标是（-3，1）；

∵B（-4，2），-4＜2，

∴点B的对应点的坐标为（-2，-4），

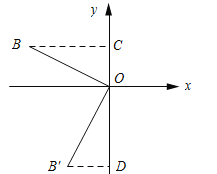
过点B作BC⊥y轴，垂足为C，

过点作D⊥y轴，垂足为D，

，

,

在和中，

，

∴≌（SAS），

，

，

，

故，

故答案为：（-3，1）；90；

（2）设点F的坐标为（x，-2x-6），

当x＞-2x-6时，

解得：x＞-2，

不合题意，舍去；

当x≤-2x-6时，

解得：x＜-2，

符合题意；

∵F（x，-2x-6），且x≤-2x-6，

∴，

，

，

∴当时，

有最小值，

当时，

有最大值，

∴的取值范围为：；

（3）由题意得的顶点E的坐标为E（-2，m），m＞0，

∵点P的坐标在上，

∴设点P的坐标为，

①若，

则点，

点恰好在抛物线的对称轴上，且四边形是菱形，

则，

∴m=8，符合题意；

②若，

则点，

点恰好在抛物线的对称轴上，且四边形是菱形，

则，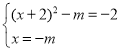

∴m=2或m=3，符合题意；

综上所述，m=8或m=2或m=3．