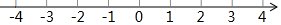题目内容
5．解不等式组$\left\{\begin{array}{l}x+1≥2①\\ 5x≤4x+3②\end{array}\right.$请结合题意填空，完成本题的解答．
（1）解不等式①，得x≥1；
（2）解不等式②，得x≤3；
（3）把不等式①和②的解集在数轴上表示出来：
（4）原不等式组的解集为1≤x≤3．
分析 分别求出每一个不等式的解集，根据各不等式解集在数轴上的表示，由公共部分即可确定不等式组的解集．
解答 解：（1）解不等式①，得：x≥1；
（2）解不等式②，得：x≤3；
（3）把不等式①和②的解集在数轴上表示出来：
（4）原不等式组的解集为1≤x≤3，
故答案为：x≥1，x≤3，1≤x≤3．
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
相关题目
15．2的算术平方根是（ ）
| A． | $±\sqrt{2}$ | B． | $\sqrt{2}$ | C． | $-\sqrt{2}$ | D． | 2 |
16．下列运算正确的是（ ）
| A． | a-（b+c）=a-b+c | B． | 2a2•3a3=6a5 | C． | a3+a3=2a6 | D． | （x+1）2=x2+1 |
13．cos60°的值等于（ ）
| A． | $\sqrt{3}$ | B． | 1 | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{1}{2}$ |
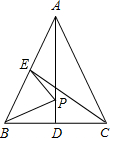如图，在△ABC中，AB=AC，AD、CE是△ABC的两条中线，P是AD上一个动点，则下列线段的长度等于BP+EP最小值的是（ ）
