题目内容
已知两抛物线y=-x2+3x+1与y=-2x2+x+1,请至少写出三条它们的共同特点.
考点:二次函数的性质
专题:
分析:根据二次系数的符号相同得到它们的开口都向下,根据对称轴方程可得两抛物线的对称轴都在y轴的右侧;根据c相同得到它们与y轴的交点都是(0,1).
解答:解:抛物线y=-x2+3x+1与抛物线y=-2x2+x+1的开口都向下,两抛物线的对称轴都在y轴的右侧;它们与y轴的交点都是(0,1).
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一天早晨的气温是-7℃,中午的气温比早晨上升10℃,中午的气温是( )
| A、10℃ | B、17℃ |
| C、3℃ | D、-10℃ |
若a-3=-3,-5是b的相反数,则a与b的和是( )
| A、-5 | B、-1 | C、1 | D、5 |
 如图,在?ABCD中,AE⊥BC于E点,点E为BC的中点,tanB=2,点P在BE上,作EF⊥DP于点F,连结AF.
如图,在?ABCD中,AE⊥BC于E点,点E为BC的中点,tanB=2,点P在BE上,作EF⊥DP于点F,连结AF. 如图,正方形ABCD是圆的内接正方形,点P是圆周上(不同于B,C)任意一点,则∠BPC的度数是
如图,正方形ABCD是圆的内接正方形,点P是圆周上(不同于B,C)任意一点,则∠BPC的度数是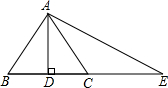 如图,AB=AC,AD⊥BC,点C在线段AE的垂直平分线上,在不添加任何线或字母情况下,问AB+BD会与图中哪条线段相等?答:是
如图,AB=AC,AD⊥BC,点C在线段AE的垂直平分线上,在不添加任何线或字母情况下,问AB+BD会与图中哪条线段相等?答:是