题目内容
14．矩形的两邻边长的差为2，对角线长为4，则矩形的面积为（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 10 |
分析 设矩形一条边长为x，则另一条边长为x-2，然后根据勾股定理列出方程式求出x的值，继而可求出矩形的面积．
解答 解：设矩形一条边长为x，则另一条边长为x-2，
由勾股定理得，x2+（x-2）2=42，
整理得，x2-2x-6=0，
解得：x=1+$\sqrt{7}$或x=1-$\sqrt{7}$（不合题意，舍去），
另一边为：$\sqrt{7}$-1，
则矩形的面积为：（1+$\sqrt{7}$）（$\sqrt{7}$-1）=6．
故选B．
点评 本题考查了勾股定理及矩形的性质，难度适中，解答本题的关键是根据勾股定理列出等式求处矩形的边长，要求同学们掌握矩形面积的求法．
练习册系列答案
相关题目
如图，在△ABC中，AB=AC=6cm，∠B=15°，CD是AB边上的高，则△ABC的面积是9cm2．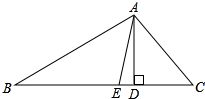
已知，如图在△ABC中，AD，AE分别是△ABC的高和角平分线，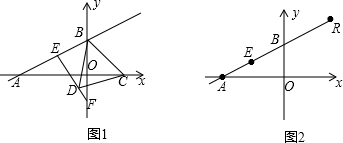
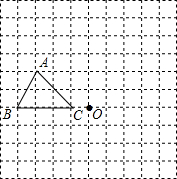19．若分式$\frac{|x|-3}{{x}^{2}-2x-3}$的值为零，则x的值是（ ）
| A． | 3 | B． | -3 | C． | ±3 | D． | 0 |
在如图的方格纸中，每个小方格都是边长为1个单位的正方形，△ABC的三个顶点都在格点上．