题目内容
在Rt△ABC中，若∠C=90°，AC=4，BC=2，则tanB= ．
考点：锐角三角函数的定义
专题：
分析：由正切的定义可知tanB=
，代入计算即可．
| AC |
| BC |
解答：解：
∵∠C=90°，AC=4，BC=2，
∴tanB=
=
=2，
故答案为：2．
∵∠C=90°，AC=4，BC=2，
∴tanB=
| AC |
| BC |
| 4 |
| 2 |
故答案为：2．
点评：本题主要考查三角函数的定义，掌握正切的定义是解题的关键．
练习册系列答案
相关题目
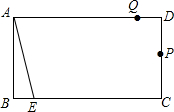如图，矩形ABCD中，AB=6cm，BC=10cm，动点P从点D出发，按折线DCBAD方向以2cm/s的速度运动，动点Q从点D出发，按折线DABCD方向以1cm/s的速度运动，当点P运动到点D时，点Q随之停止运动．若点E在线段BC上，且BE=1cm，若动点P、Q同时出发，经过几秒钟，点A、E、P、Q组成平行四边形？
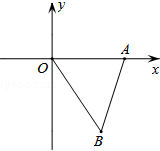如图，平面直角坐标系xOy中，点A、B的坐标分别为（3，0）、（2，-3），△EFD是△ABO关于原点O的位似图形，且原图形与它位似比为2，则点F的坐标为∠A，∠B，∠C是△ABC的三个内角，则sin
等于（ ）
| A+B |
| 2 |
A、cos
| ||
B、sin
| ||
| C、cosC | ||
D、cos
|
如图，点A、D、G、M在半圆上，四边形ABOC、DEOF、HMNO均为矩形，设BC=a，EF=b，HN=c，则a、b、c三者间的大小关系为在△ABC中，AD为∠BAC的平分线，DE⊥AB，F为AC上一点，且∠DFA=120°，则DE与DF的关系为（自己画图）（ ）
| A、DE＞DF |
| B、DE＜DF |
| C、DE=DF |
| D、不能确定DE与DF的大小 |