题目内容
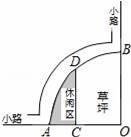
如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )

A.(10π﹣
 )米2 B.(π﹣
)米2 B.(π﹣
 )米2 C.(6π﹣
)米2 C.(6π﹣
 )米2 D.(6π﹣
)米2 D.(6π﹣
 )米2
)米2
C【考点】扇形面积的计算.
【专题】压轴题;探究型.
【分析】先根据半径OA长是6米,C是OA的中点可知OC=
 OA=3,再在Rt△OCD中,利用勾股定理求出CD的长,根据锐角三角函数的定义求出∠DOC的度数,由S阴影=S扇形AOD﹣S△DOC即可得出结论.
OA=3,再在Rt△OCD中,利用勾股定理求出CD的长,根据锐角三角函数的定义求出∠DOC的度数,由S阴影=S扇形AOD﹣S△DOC即可得出结论.
【解答】解:连接OD,
∵弧AB的半径OA长是6米,C是OA的中点,
∴OC=
 OA=
OA=
 ×6=3米,
×6=3米,
∵∠AOB=90°,CD∥OB,
∴CD⊥OA,
在Rt△OCD中,
∵OD=6,OC=3,
∴CD=
 =
=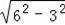
 =3
=3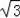
 米,
米,
∵sin∠DOC=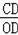
 =
=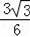
 =
=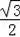
 ,
,
∴∠DOC=60°,
∴S阴影=S扇形AOD﹣S△DOC=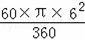
 ﹣
﹣
 ×3×3
×3×3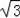
 =(6π﹣
=(6π﹣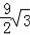
 )平方米.
)平方米.
故选C.


【点评】本题考查的是扇形的面积,根据题意求出∠DOC的度数,再由S阴影=S扇形AOD﹣S△DOC得出结论是解答此题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目


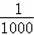
 x2+
x2+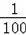
 x(x>0),若该车某次的刹车距离为9m,则开始刹车时的速度为 m/s.
x(x>0),若该车某次的刹车距离为9m,则开始刹车时的速度为 m/s.




 的结果为( )
的结果为( )