题目内容
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象.当快车到达甲地时,慢车离甲地的距离为 千米.
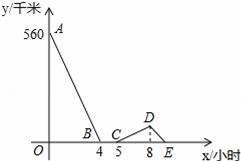

60 千米.
【考点】一次函数的应用.
【分析】先根据题意得出慢车往返分别用了4小时,慢车行驶4小时的距离,快车3小时即可行驶完,进而求出快车速度以及利用两车速度之比得出慢车速度;再求出快车到达甲地用时,即可求出快车到达甲地时慢车据甲地的距离.
【解答】解:由题意可得出:慢车和快车经过4个小时后相遇,相遇后停留了1个小时,出发后两车之间的距离开始增大,快车到达甲地后两车之间的距离开始缩小,由图分析可知快车经过3个小时后到达甲地,此段路程慢车需要行驶4小时,因此慢车和快车的速度之比为3:4,
∴设慢车速度为3xkm/h,快车速度为4xkm/h,
∴(3x+4x)×4=560,x=20,
∴快车的速度是80km/h,慢车的速度是60km/h.
快车和慢车相遇地离甲地的距离为4×60=240km,
当慢车行驶了7小时后,快车已到达甲地,此时两车之间的距离为240﹣3×60=60km.
故答案为60.
【点评】本题主要考查的是函数图象的应用,根据图象得出相应的信息是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,其中
,其中 ,
, .
.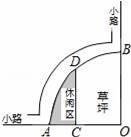


 )米2 B.(π﹣
)米2 B.(π﹣
 )米2
)米2
 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )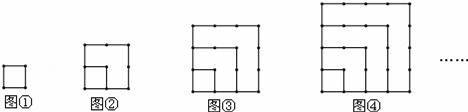

 的次数是( )
的次数是( ) 3 B、4 C、5 D、6
3 B、4 C、5 D、6 )
)