题目内容
关于x的方程(a﹣5)x2﹣4x﹣1=0有实数根,则a满足( )
A.a≥1 B.a>1且a≠5 C.a≥1且a≠5 D.a≠5
A【考点】根的判别式.
【专题】判别式法.
【分析】由于x的方程(a﹣5)x2﹣4x﹣1=0有实数根,那么分两种情况:(1)当a﹣5=0时,方程一定有实数根;(2)当a﹣5≠0时,方程成为一元二次方程,利用判别式即可求出a的取值范围.
【解答】解:分类讨论:
①当a﹣5=0即a=5时,方程变为﹣4x﹣1=0,此时方程一定有实数根;
②当a﹣5≠0即a≠5时,
∵关于x的方程(a﹣5)x2﹣4x﹣1=0有实数根
∴16+4(a﹣5)≥0,
∴a≥1.
∴a的取值范围为a≥1.
故选:A.
【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根;切记不要忽略一元二次方程二次项系数不为零这一隐含条件.

练习册系列答案
相关题目
为了估计某市空气质量情况,某同学在30天里做了如下记录:
| 污染指数(w) | 40 | 60 | 80 | 100 | 120 | 140 |
| 天数(天) | 3 | 5 | 10 | 6 | 5 | 1 |
其中w<50时空气质量为优,50≤w≤100时空气质量为良,100<w≤150时空气质量为轻度污染,若1年按365天计算,请你估计该城市在一年中空气质量达到良以上(含良)的天数为 天.
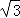 ,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )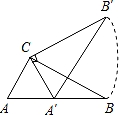
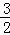 π B.
π B.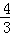
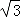 π C.2π D.3π
π C.2π D.3π
 B.﹣5 C.±5 D.﹣
B.﹣5 C.±5 D.﹣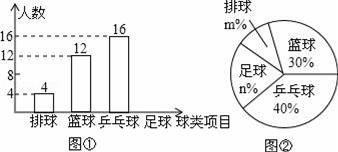

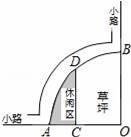


 )米2 B.(π﹣
)米2 B.(π﹣
 )米2
)米2