题目内容
如图1,矩形 ,
, 为原点,点
为原点,点 在
在 上,把
上,把 沿
沿 折叠,使点
折叠,使点 落在
落在 边上的点
边上的点 处,A、D坐标分别为
处,A、D坐标分别为 和
和 ,抛物线
,抛物线 过点
过点 .
.
(1)求 点的坐标及该抛物线的解析式;
点的坐标及该抛物线的解析式;
(2)如图2,矩形 的长、宽一定,点
的长、宽一定,点 沿(1)中的抛物线滑动,在滑动过程中
沿(1)中的抛物线滑动,在滑动过程中 轴,且
轴,且 在
在 的下方,当
的下方,当 点横坐标为-1时,点
点横坐标为-1时,点 位于
位于 轴上方且距离
轴上方且距离 轴
轴 个单位.当矩形
个单位.当矩形 在滑动过程中被
在滑动过程中被 轴分成上下两部分的面积比为2:3时,求点
轴分成上下两部分的面积比为2:3时,求点 的坐标;
的坐标;
(3)如图3,动点 同时从点
同时从点 出发,点
出发,点 以每秒3个单位长度的速度沿线段
以每秒3个单位长度的速度沿线段 运动,点
运动,点 以每秒8个单位长度的速度沿折线
以每秒8个单位长度的速度沿折线 按
按 的路线运动,当
的路线运动,当 中的其中一点停止运动时,另一点也停止运动.设
中的其中一点停止运动时,另一点也停止运动.设 同时从点
同时从点 出发秒时,
出发秒时, 的面积为
的面积为 .求
.求 与的函数关系式,并写出的取值范围.
与的函数关系式,并写出的取值范围.
解:(1) 由矩形 得
得 ,
, ,
, 
由 沿
沿 翻折得到
翻折得到 ,得
,得 
由勾股定理得: 
得  ,
, 
又 均在
均在 上代入得
上代入得

(2)当 时,
时, ,此时
,此时
又由 距离
距离 轴上方
轴上方 个单位, 得
个单位, 得
 矩形
矩形 的长为8.
的长为8.
设 在下滑过程中交
在下滑过程中交 轴分别于
轴分别于 两点.
两点.
则由题意知: 即
即

故 的纵坐标为
的纵坐标为 ,设
,设 ,则
,则
得
 或
或
(3)①当 时,此时
时,此时 在
在 上,
上, 在
在 上.
上.
②当 时,此时
时,此时 在
在 上,
上, 在
在 上.则
上.则
过 作
作 于
于
则 得
得





解析

练习册系列答案
相关题目
 四边形OABC是矩形,若反比例函数
四边形OABC是矩形,若反比例函数 这条抛物线所对应的函数关系式.
这条抛物线所对应的函数关系式. (2013•宝应县模拟)如图,在以O为原点的直角坐标系中,点A、C分别在x轴、y轴的正半轴上,点B在第一象限,四边形OABC是矩形,反比例函数y=
(2013•宝应县模拟)如图,在以O为原点的直角坐标系中,点A、C分别在x轴、y轴的正半轴上,点B在第一象限,四边形OABC是矩形,反比例函数y=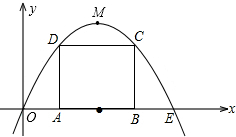 面直角坐标系.
面直角坐标系. (k>0,x>0)的图象与AB相交于点D,与BC相交于点E,且BE=CE.
(k>0,x>0)的图象与AB相交于点D,与BC相交于点E,且BE=CE.