题目内容
 在△ABC中,∠ADB=100°,∠C=80°,∠BAD=
在△ABC中,∠ADB=100°,∠C=80°,∠BAD=| 1 |
| 2 |
考点:三角形的外角性质,三角形内角和定理
专题:
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠DAC,再求出∠BAD,然后根据三角形的内角和定理求出∠ABC,再根据角平分线的定义求出∠ABE,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答:解:∵∠ADB=100°,∠C=80°,
∴∠DAC=∠ADB-∠C=100°-80°=20°,
∵∠BAD=
∠DAC,
∴∠BAD=
×20°=10°,
在△ABD中,∠ABC=180°-∠ADB-∠BAD=180°-100°-10°=70°,
∵BE平分∠ABC,
∴∠ABE=
∠ABC=
×70°=35°,
∴∠BED=∠BAD+∠ABE=10°+35°=45°.
∴∠DAC=∠ADB-∠C=100°-80°=20°,
∵∠BAD=
| 1 |
| 2 |
∴∠BAD=
| 1 |
| 2 |
在△ABD中,∠ABC=180°-∠ADB-∠BAD=180°-100°-10°=70°,
∵BE平分∠ABC,
∴∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BED=∠BAD+∠ABE=10°+35°=45°.
点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,角平分线的定义,熟记性质与定理并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列各数中,最小的是( )
| A、-2 | ||
| B、0 | ||
C、-
| ||
| D、3 |
 如图,已知AC=8cm,点B为线段AC的中点,点P从A出发以2cm/s的速度沿A-B-C的路径向终点C运动,P点运动时间为t,求:t取何值时,PB=3PC.
如图,已知AC=8cm,点B为线段AC的中点,点P从A出发以2cm/s的速度沿A-B-C的路径向终点C运动,P点运动时间为t,求:t取何值时,PB=3PC.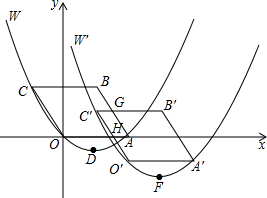 综合与探究:如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,A、C两点的坐标分别为(4,0),(-2,3),抛物线W经过O、A、C三点,D是抛物线W的顶点.
综合与探究:如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,A、C两点的坐标分别为(4,0),(-2,3),抛物线W经过O、A、C三点,D是抛物线W的顶点.