题目内容
10. 如图,△ABC的三边长为AC=5,BC=6,AB=7,⊙O与△ABC的三边相切于D,E,F.
如图,△ABC的三边长为AC=5,BC=6,AB=7,⊙O与△ABC的三边相切于D,E,F.(1)求AF、BD、CE的长;
(2)若⊙O的半径为2,求△ABC的面积.
分析 (1)设AF=x,由切线长定理可知AE=AF=x,则EC=DC=5-x,BD=BF=7-x,最后根据DB+CD=6列方程求解即可;
(2)依据△ABC的面积=$\frac{1}{2}×$△ABC的周长×内切圆的半径求解即可.
解答 解:(1)设AF=x,由切线长定理可知:AE=AF=x,则EC=DC=5-x,BD=BF=7-x.
∵DB+CD=6,
∴5-x+7-x=6.
解得:x=3.
∴AF=3,BD=7-3=4,CE=5-3=2.
∴AF=3,BD=4,CE=2.
(2)${S}_{△ABC}=\frac{1}{2}×(5+6+7)×2$=18.
点评 本题主要考查的是三角形的内切圆与内心,依据切线长定理列出关于x的方程是解题的关键.

练习册系列答案
相关题目
20. 如图所示,△ABC∽△ACD,且AB=10cm,AC=8cm,则AD的长是( )
如图所示,△ABC∽△ACD,且AB=10cm,AC=8cm,则AD的长是( )
 如图所示,△ABC∽△ACD,且AB=10cm,AC=8cm,则AD的长是( )
如图所示,△ABC∽△ACD,且AB=10cm,AC=8cm,则AD的长是( )| A. | 6.4cm | B. | 6cm | C. | 2cm | D. | 4cm |
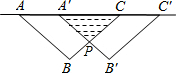 如图,把等腰Rt△ABC沿AC方向平移到等腰Rt△A′B′C′的位置时,它们重叠的部分的面积是Rt△ABC面积的$\frac{1}{4}$.若AB=$\sqrt{2}$cm,则它移动的距离AA′=1cm.
如图,把等腰Rt△ABC沿AC方向平移到等腰Rt△A′B′C′的位置时,它们重叠的部分的面积是Rt△ABC面积的$\frac{1}{4}$.若AB=$\sqrt{2}$cm,则它移动的距离AA′=1cm.