题目内容
9.已知在△ABC中,∠A比2∠B多10°,∠B比2∠C少10°,则∠A=($\frac{730}{7}$)°,∠B=($\frac{330}{7}$)°.分析 根据已知得出∠B=2∠C-10°,∠A=4∠C-10°,代入∠A+∠B+∠C=180°求出即可.
解答 解: ∵∠A比2∠B大10°,∠B比2∠C少10°,
∵∠A比2∠B大10°,∠B比2∠C少10°,
∴∠A-2∠B=10°,∠B=2∠C-10°,
∴∠A=10°+2∠B=10°+2(2∠C-10°)=4∠C-10°,
∵∠A+∠B+∠C=180°,
∴4∠C-10°+2∠C-10°+∠C=180°,
∴∠C=$\frac{200}{7}$°,
∴∠A=4×($\frac{200}{7}$)°-10°=($\frac{730}{7}$)°,∠B=2×($\frac{200}{7}$)°-10°=($\frac{330}{7}$)°.
故答案为:($\frac{730}{7}$)°,($\frac{330}{7}$)°.
点评 此题考查了三角形内角和定理的应用,注意:三角形的内角和等于180°,渗透方程思想.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
20.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
| A. | 当AB=BC时,它是菱形 | B. | 当∠ABC=90°时,它是矩形 | ||
| C. | 当AC=BD时,它是正方形 | D. | 当AC⊥BD时,它是菱形 |
4.某汽车出租公司为扩大业务,准备购置10辆客车,通过市场调查得到以下信息:
(1)现公司预计用390万元购买两种客车,每种客车可以买多少辆?
(2)如果公司可用的购车资金为380~400万元(含380万元和400万元),为使公司日收入最大,应如何确定购车方案?
| 客车 | 座位 | 售价(万元) | 每座日租金(元) | 出租率 |
| 大型 | 40 | 45 | 80 | 55% |
| 中型 | 25 | 35 | 80 | 70% |
(2)如果公司可用的购车资金为380~400万元(含380万元和400万元),为使公司日收入最大,应如何确定购车方案?
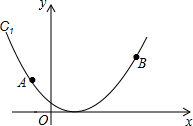 如图,在平面直角坐标系中,过点A(-2,2),点B(4,4)的抛物线C1的函数表达式y=ax2+bx.求抛物线C1的函数表达式及其对称轴.
如图,在平面直角坐标系中,过点A(-2,2),点B(4,4)的抛物线C1的函数表达式y=ax2+bx.求抛物线C1的函数表达式及其对称轴. 如图,已知AD是等边△ABC的中线,点E是AB的点,且AE=AD,求∠EDB的度数.
如图,已知AD是等边△ABC的中线,点E是AB的点,且AE=AD,求∠EDB的度数.