题目内容
1.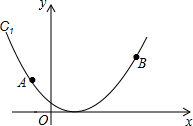 如图,在平面直角坐标系中,过点A(-2,2),点B(4,4)的抛物线C1的函数表达式y=ax2+bx.求抛物线C1的函数表达式及其对称轴.
如图,在平面直角坐标系中,过点A(-2,2),点B(4,4)的抛物线C1的函数表达式y=ax2+bx.求抛物线C1的函数表达式及其对称轴.
分析 把点A(-2,2),点B(4,4)代入y=ax2+bx,得到方程组,求出a,b,即可求得抛物线C1的函数表达式,进而根据对称轴公式即可求得对称轴.
解答 解:∵抛物线y=ax2+bx(a≠0)过点A(-2,2),点B(4,4),
∴$\left\{\begin{array}{l}{4a-2b=2}\\{16a+4b=4}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=-\frac{1}{3}}\end{array}\right.$,
∴抛物线的函数关系式为y=$\frac{1}{3}$x2-$\frac{1}{3}$x;
∴抛物线y=$\frac{1}{3}$x2-$\frac{1}{3}$x的对称轴为直线x=-$\frac{b}{2a}$=$\frac{-\frac{1}{3}}{2×\frac{1}{3}}$=-$\frac{1}{2}$.
点评 本题考查了待定系数法求二次函数的解析式以及对称轴,熟练掌握待定系数法是解题的关键.

练习册系列答案
相关题目
11.为了了解某小区居民的用水情况,随机抽查了该小区10户家庭的月用水量,结果如下:
(1)计算这家庭的平均月用水量;
(2)如果该小区有500户家庭,根据上面的计算结果,估计该小区居民每月共用水多少吨?
| 月用水量(吨) | 10 | 13 | 14 | 17 | 18 |
| 户数 | 2 | 2 | 3 | 2 | 1 |
(2)如果该小区有500户家庭,根据上面的计算结果,估计该小区居民每月共用水多少吨?
12.若平行四边形中两个内角的度数比为1:3,则其中较小的内角是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
13.直线y=(3m-2)${x}^{{m}^{2}-3}$的图象在第二、四象限,则m的值是( )
| A. | 2 | B. | -2 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |