��Ŀ����
17���̲���̽��ƽ���ʽʱ���������������������˿��������Ǽ��乫ʽ��������ֱ�۵��Ƶ�����֤��ʽ���׳ơ�����֤���������磬��������ˬ��ͼ����ͼ�٣������ĸ�ֱ�������νϴ��ֱ�DZ߳���Ϊa����С��ֱ�DZ߳���Ϊb��б�߳���Ϊc�����������ε�������Ա�ʾΪc2��Ҳ���Ա�ʾΪ4��$\frac{1}{2}ab+{��a-b��^2}$�ɴ��Ƶ�����Ҫ�Ĺ��ɶ��������ֱ������������ֱ�DZ߳�Ϊa��b��б�߳�Ϊc����a2+b2=c2��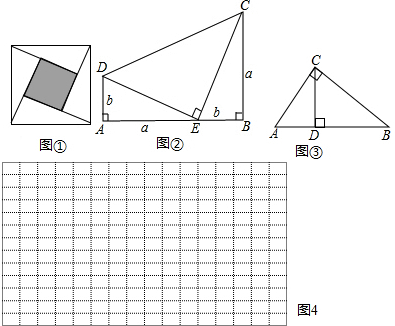
��1��ͼ��Ϊ�����ڶ�ʮ����ͳ٤�ƶ��µġ���ͳ֤��������������ͼ���Ƶ����ɶ�����
��2����ͼ�ۣ�ֱ�ǡ�ABC�У���ACB=90�㣬AC=3cm��BC=4cm����б��AB�ϵĸ�CD�ij�Ϊ$\frac{12}{5}$cm��
��3���Թ���һ��ͼ�Σ�ʹ��������ܹ����ͣ�a+b����a+2b��=a2+3ab+2b2��������ͼ4�������У��������ĸa��b����ʾ���߶Σ�
���� ��1�����ε�������������ε������ʽ�����Ҳ����������ֱ��������������������������������г���ϵʽ�����ɵ�֤��
��2����֪��ֱ�DZߣ����ù��ɶ������б�߳���������������������б���ϵĸߣ�
��3����֪ͼ������ı���ʽ�����ɸ��ݱ���ʽ�ó�ͼ�εı߳��ı���ʽ�����ɻ���ͼ�Σ�
��� �⣺��1������ABCD�����Ϊ$\frac{1}{2}$��a+b����a+b��=$\frac{1}{2}$a2+ab+$\frac{1}{2}$b2��
Ҳ�����ñ�ʾΪ$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$ab��
��$\frac{1}{2}$a2+ab+$\frac{1}{2}$b2=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$ab����a2+b2=c2
��2����ֱ�������ε���ֱ�DZ߷ֱ�Ϊ3��4��
��б��Ϊ5��
����б���ϵĸ�Ϊh��ֱ�������ε����Ϊ$\frac{1}{2}$��3��4=$\frac{1}{2}$��5��h��
��h=$\frac{12}{5}$��
��3����ͼ�����Ϊ����a+b����a+2b��=a2+3ab+2b2��
��߳�Ϊ��a+2b����a+b����
�ɴ˿ɻ�����ͼ��Ϊ��
���� ���⿼���˹��ɶ�����֤�������ɶ���������ʽ�ij˷��������Լ��ɶ���ʽ��ͼ�εĴ������ͣ�����֤��Ҫת����ͬһ�����������ֱ�ʾ�������Ӷ�ת���ɷ��̴ﵽ֤���Ľ����

 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д� �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д�| A�� | ��a3��2=a6 | B�� | a3•a2=a6 | C�� | a8��a2=a4 | D�� | a+2a2=3a2 |
| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | 75�� |
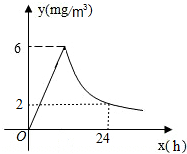 ÿ�괺��ΪԤ�����У�ijУ������Ϣ�նԽ��ҽ���ҩѬ��������֪ҩ��ȼ�չ��̼�ȼ���������еĺ�ҩ��y��mg/m3����ʱ��x��h��֮��Ĺ�ϵ��ͼ��ʾ����������Ҫ�����еĺ�ҩ��������3mg/m3�ҳ���ʱ�䲻�ܵ���10h�������������һ�£��������еĺ�ҩ��������3mg/m3ʱ������ʱ����Դﵽ12h��
ÿ�괺��ΪԤ�����У�ijУ������Ϣ�նԽ��ҽ���ҩѬ��������֪ҩ��ȼ�չ��̼�ȼ���������еĺ�ҩ��y��mg/m3����ʱ��x��h��֮��Ĺ�ϵ��ͼ��ʾ����������Ҫ�����еĺ�ҩ��������3mg/m3�ҳ���ʱ�䲻�ܵ���10h�������������һ�£��������еĺ�ҩ��������3mg/m3ʱ������ʱ����Դﵽ12h�� ��ͼ���ı���ABCD�ڽ���ԲO������B=77�㣬���D=103�㣮
��ͼ���ı���ABCD�ڽ���ԲO������B=77�㣬���D=103�㣮