题目内容
 如图,在△ABC中,CD⊥AB,垂足为点D,已知AC=4,BC=3,BD=
如图,在△ABC中,CD⊥AB,垂足为点D,已知AC=4,BC=3,BD=| 9 |
| 5 |
考点:勾股定理的逆定理,勾股定理
专题:证明题
分析:在Rt△BCD中,先由勾股定理求出CD的长,然后在RtACD中,由勾股定理再求出AD的长,进而求出AB的长,然后在△ABC中,再利用勾股定理的逆定理证明即可.
解答:证明:∵CD⊥AB,
∴△ACD和△BCD都是直角三角形,
Rt△BCD中,
∵BC=3,BD=
,
∴由勾股定理得:CD=
=
,
在Rt△ACD中,
∵AC=4,
∴由勾股定理得:AD=
=
,
∴AB=AD+BD=5,
∵AC2+BC2=25=52=AB2,
∴△ABC是直角三角形.
∴△ACD和△BCD都是直角三角形,
Rt△BCD中,
∵BC=3,BD=
| 9 |
| 5 |
∴由勾股定理得:CD=
| BC2-BD2 |
| 12 |
| 5 |
在Rt△ACD中,
∵AC=4,
∴由勾股定理得:AD=
| AC2-CD2 |
| 16 |
| 5 |
∴AB=AD+BD=5,
∵AC2+BC2=25=52=AB2,
∴△ABC是直角三角形.
点评:本题考查了勾股定理,勾股定理逆定理,根据图形判断出所求的边所在的直角三角形是解题的关键.

练习册系列答案
相关题目
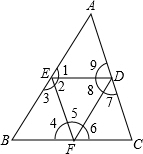 如图,填空:
如图,填空: 如图,在△ABC中,∠C=90°,∠A=30°,DE垂直平分AB交AC于D,交AB于E,若DE=1.5cm,求AC的长.
如图,在△ABC中,∠C=90°,∠A=30°,DE垂直平分AB交AC于D,交AB于E,若DE=1.5cm,求AC的长.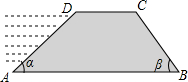 如图,拦水坝的横断面为梯形ABCD,已知上底DC=5m,迎水面坡度为1:
如图,拦水坝的横断面为梯形ABCD,已知上底DC=5m,迎水面坡度为1: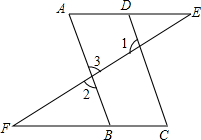 如图,已知∠1+∠2=180°,∠A=∠C,试判断AE与CF的位置关系,并说明理由.
如图,已知∠1+∠2=180°,∠A=∠C,试判断AE与CF的位置关系,并说明理由. 如图,?ABCD中,C在x轴上,点A为(2,3),AC交OB于D,?ABCO的面积为18,则D的坐标为
如图,?ABCD中,C在x轴上,点A为(2,3),AC交OB于D,?ABCO的面积为18,则D的坐标为 如图,已知DE∥BC,EF平分∠AED,EF⊥AB,CD⊥AB,试说明CD平分∠ACB.
如图,已知DE∥BC,EF平分∠AED,EF⊥AB,CD⊥AB,试说明CD平分∠ACB.