题目内容
 细心观察图形,认真分析各式,然后解答问题.
细心观察图形,认真分析各式,然后解答问题.OA22=(
| 1 |
| ||
| 2 |
OA32=12+(
| 2 |
| ||
| 2 |
OA42=12+(
| 3 |
| ||
| 2 |
(1)推算出OA10的长=
(2)若一个三角形的面积是
| 5 |
(3)用含n(n是正整数)的等式表示上述变化规律;
(4)求出S12+S22+S32+…+S102的值.
考点:勾股定理
专题:规律型
分析:(1)根据题中给出的规律即可得出结论;
(2)若一个三角形的面积是
,利用前面公式可以得到它是第几个三角形;
(3)利用已知可得OAn2,注意观察数据的变化;
(4)将前10个三角形面积相加,利用数据的特殊性即可求出.
(2)若一个三角形的面积是
| 5 |
(3)利用已知可得OAn2,注意观察数据的变化;
(4)将前10个三角形面积相加,利用数据的特殊性即可求出.
解答:解:(1))∵OAn2=n,
∴OA10=
.
故答案为:
;
(2)若一个三角形的面积是
,
∵Sn=
=
,
∴
=2
=
,
∴它是第20个三角形.
故答案为:20;
(3)结合已知数据,可得:OAn2=n;Sn=
;
(4)S12+S22+S32+…+S102
=
+
+
+
+…+
=
=
=
.
∴OA10=
| 10 |
故答案为:
| 10 |
(2)若一个三角形的面积是
| 5 |
∵Sn=
| ||
| 2 |
| 5 |
∴
| n |
| 5 |
| 20 |
∴它是第20个三角形.
故答案为:20;
(3)结合已知数据,可得:OAn2=n;Sn=
| ||
| 2 |
(4)S12+S22+S32+…+S102
=
| 1 |
| 4 |
| 2 |
| 4 |
| 3 |
| 4 |
| 4 |
| 4 |
| 10 |
| 4 |
=
| 1+2+1+…+10 |
| 4 |
=
| 5×10+5 |
| 4 |
=
| 55 |
| 4 |
点评:本题考查的是勾股定理,涉及到数据的规律性,综合性较强,希望同学们能认真的分析总结数据的特点.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
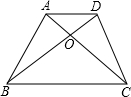 如图,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于点O,∠ABC=75°,则△AOD与△BOC的面积之比( )
如图,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于点O,∠ABC=75°,则△AOD与△BOC的面积之比( )| A、1:2 | ||
B、1:
| ||
| C、1:3 | ||
| D、1:4 |
下列说法中,正确的是( )
| A、-an和(-a)n一定不相等 |
| B、-an和(-a)n一定互为相反数 |
| C、当n为奇数时,-an和(-a)n相等 |
| D、当n为偶数时,-an和(-a)n相等 |
 如图,在△ABC中,AB=AC,D是BC的中点,DF⊥AC,E是DF的中点,联结AE、BF.求证:(1)DF2=CF•AF; (2)AE⊥BF.
如图,在△ABC中,AB=AC,D是BC的中点,DF⊥AC,E是DF的中点,联结AE、BF.求证:(1)DF2=CF•AF; (2)AE⊥BF. 如图,DE,FG分别是△ABC的AB,AC边的垂直平分线,连接AG,AE,已知BC=10,GE=2,∠BAC=80°,则∠GAE=
如图,DE,FG分别是△ABC的AB,AC边的垂直平分线,连接AG,AE,已知BC=10,GE=2,∠BAC=80°,则∠GAE=