题目内容
13..先化简,再求值:($\frac{b}{a+b}$+$\frac{b}{a-b}$)÷$\frac{a}{{a}^{2}-{b}^{2}}$,其中a=2017,b=$\sqrt{2}$.分析 根据分式的加法和除法可以化简题目中的式子,然后将a、b的值代入即可解答本题.
解答 解:($\frac{b}{a+b}$+$\frac{b}{a-b}$)÷$\frac{a}{{a}^{2}-{b}^{2}}$
=$\frac{b(a-b)+b(a+b)}{(a+b)(a-b)}•\frac{(a+b)(a-b)}{a}$
=$\frac{ab-{b}^{2}+ab+{b}^{2}}{a}$
=2b,
当a=2017,b=$\sqrt{2}$时,原式=2$\sqrt{2}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.若$\sqrt{a-3}$在实数范围内有意义,则a的取值范围是( )
| A. | a≤3 | B. | a≥3 | C. | a≤-3 | D. | a≥-3 |
1.据海关统计,2016年前7个月,我国进出口总值132100亿元人民币,将132100用科学记数法表示为( )
| A. | 1321×102 | B. | 0.1321×104 | C. | 1.321×105 | D. | 0.1321×106 |
8.若点A(a+1,b-1)在第二象限,则点B(-1,b)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
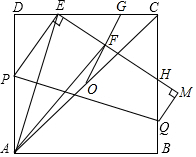 已知正方形ABCD,点P、Q分别是边AD、BC上的两动点,将四边形ABQP沿PQ折叠得到四边形EMQP,点E刚好落在CD边上,且DE=3,EF交BC于点H,连接AE,过点A作AF⊥EH于点F,取对角线AC的中点O,连接OF并延长交CD于点G,△ECH周长为18,则△EFG的周长为6+$\frac{3}{5}$$\sqrt{10}$.
已知正方形ABCD,点P、Q分别是边AD、BC上的两动点,将四边形ABQP沿PQ折叠得到四边形EMQP,点E刚好落在CD边上,且DE=3,EF交BC于点H,连接AE,过点A作AF⊥EH于点F,取对角线AC的中点O,连接OF并延长交CD于点G,△ECH周长为18,则△EFG的周长为6+$\frac{3}{5}$$\sqrt{10}$.