题目内容
解不等式组
，并把解集表示在数轴上．
|
考点：解一元一次不等式组,在数轴上表示不等式的解集
专题：
分析：先求出两个不等式的解集，再求其公共解．
解答：解：解不等式①得，x＜4，
解不等式②得，x＞-3，
所以不等式的解集为：-3＜x＜4，
在数轴上表示为：
解不等式②得，x＞-3，
所以不等式的解集为：-3＜x＜4，
在数轴上表示为：
点评：此题考查一元一次不等式组的解法．借助数轴确定不等式组的解集很关键．不等式组的解集：不等式组的解集可以先求这些个不等式各自的解，然后再找它们的相交的公共部分（最好先在数轴上画出它们的解），找它们的相交的公共部分可以用这个口诀记住：同小取小，同大取大；比大的小，比小的大，取中间；比大的大，比小的小，无解．
练习册系列答案
相关题目
如图，在△ABC中，∠A=75°，∠B=30°，则∠ACD=
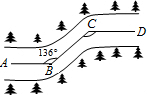一条公路两次转弯后又回到原来的方向（即AB∥CD，如图）如果第一次转弯时∠B=136°，那么∠C应是（ ）| A、136° | B、124° |
| C、144° | D、154° |
如图，在直角梯形ABCD中，AB⊥BC．EF是梯形的中位线，AB∥DH．AD=1．BC=3，CD=4．有下列4个结论：①∠BCD=60°，②EH=2，③四边形EHCF是菱形，④△EHB∽△CEB．其中正确的有（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
在平面直角坐标系中，点（-5，2）所在的象限为（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |