题目内容
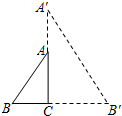 如图,在Rt△ABC中,∠ACB=90°,AB=5,cosB=
如图,在Rt△ABC中,∠ACB=90°,AB=5,cosB=| 3 |
| 5 |
考点:旋转的性质
专题:计算题
分析:在Rt△ABC中,根据余弦的定义得到cosB=
=
,则可得到BC=3,再利用勾股定理计算出AC=4,由于∠BAA′>90°,△AA′B是等腰三角形,所以只有AA′=AB=5,则A′C=AA′+AC=9,再根据折叠和位似的性质得∠B′=∠B,于是可判断Rt△A′B′C∽Rt△ABC,然后利用相似比可计算出B′C.
| BC |
| AB |
| 3 |
| 5 |
解答:解:∵Rt△ABC中,∠ACB=90°,AB=5,cosB=
,
∴cosB=
=
,即BC=3,
∴AC=
=4,
∵∠BAA′>90°,△AA′B是等腰三角形,
∴AA′=AB=5,
∴A′C=AA′+AC=5+4=9,
∵△ACB沿直线AC翻折,然后再放大得到△A′CB′,
∴∠B′=∠B,
∴Rt△A′B′C∽Rt△ABC,
∴
=
,即
=
,
∴B′C=
.
故答案为
.
| 3 |
| 5 |
∴cosB=
| BC |
| AB |
| 3 |
| 5 |
∴AC=
| AB2-BC2 |
∵∠BAA′>90°,△AA′B是等腰三角形,
∴AA′=AB=5,
∴A′C=AA′+AC=5+4=9,
∵△ACB沿直线AC翻折,然后再放大得到△A′CB′,
∴∠B′=∠B,
∴Rt△A′B′C∽Rt△ABC,
∴
| A′C |
| AC |
| B′C |
| BC |
| 9 |
| 4 |
| B′C |
| 3 |
∴B′C=
| 27 |
| 3 |
故答案为
| 27 |
| 4 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了勾股定理和相似三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
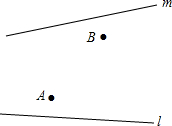 如图,在旷野上,一个人骑着马从A到B,半路上他必须先到河岸l的P点去让马饮水,然后再让马到河岸m的Q点再次饮水,最后到达B点,他应该如何选择饮马地点P、Q,才能使所走路程AP+PQ+QB为最短(假设河岸l、m为直线).
如图,在旷野上,一个人骑着马从A到B,半路上他必须先到河岸l的P点去让马饮水,然后再让马到河岸m的Q点再次饮水,最后到达B点,他应该如何选择饮马地点P、Q,才能使所走路程AP+PQ+QB为最短(假设河岸l、m为直线). 正方形ABCD中,点O是对角线AC的中点,P点为对角线AC上一动点,过点P作PF⊥DC于点F.
正方形ABCD中,点O是对角线AC的中点,P点为对角线AC上一动点,过点P作PF⊥DC于点F. 如图,AB是半圆O的直径,弦AD,BC相交于点P,且CD,AB的长分别是一元二次方程x2-7x+12=0的两根,则cos∠DPB=
如图,AB是半圆O的直径,弦AD,BC相交于点P,且CD,AB的长分别是一元二次方程x2-7x+12=0的两根,则cos∠DPB=