题目内容
在平面直角坐标系中,以坐标O1(2,0)为圆心,1为半径画圆,交x轴于A,B两点.过原点O作⊙O1的切线,
切点为M.
(1)连接MA,求证△MAO1为等边三角形.
(2)求点M的坐标.
(3)线段OM上是否存在一点P,使得以P,O,A为顶点的三角形与△OO1M相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
切点为M.
(1)连接MA,求证△MAO1为等边三角形.
(2)求点M的坐标.
(3)线段OM上是否存在一点P,使得以P,O,A为顶点的三角形与△OO1M相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
考点:圆的综合题
专题:
分析:(1)求证等边三角形,一般都是用含60°的等腰三角形证明,题中因为圆半径相等易得等腰三角形,又由坐标反应的边长的关系亦容易得60°内角,所以结果易证.
(2)求坐标即要确定其横纵坐标,适当的作垂线将其可视化是必要的,等腰三角形中三线合一易得很多边长,角度关系,又其为等边三角形,各边边长比例更是易确定,利用三角函数可以很容易的表达出各边边长,即得M点坐标.
(3)由∠MOO1=30°,使得P,O,A为顶点的三角形与△OO1M相似,则A点处的内角为90°或60°.以此建立辅助线,由特殊角30°,60°及已知边长OA=1,则两种情况的P点坐标都易得.
(2)求坐标即要确定其横纵坐标,适当的作垂线将其可视化是必要的,等腰三角形中三线合一易得很多边长,角度关系,又其为等边三角形,各边边长比例更是易确定,利用三角函数可以很容易的表达出各边边长,即得M点坐标.
(3)由∠MOO1=30°,使得P,O,A为顶点的三角形与△OO1M相似,则A点处的内角为90°或60°.以此建立辅助线,由特殊角30°,60°及已知边长OA=1,则两种情况的P点坐标都易得.
解答:(1)证明:根据题意,如图1所示,

∵M点为⊙O1切点,
∴MO1⊥OM,
在Rt△OMO1中,
∵MO1=1,OO1=2,
∴∠MOO1=30°,
∴∠MO1O=60°,
∵MO1=AO1,
∴△MAO1为等边三角形.
(2)解:如图2,过点M作MF⊥x轴,垂足为F.

∵⊙O1圆心O1的坐标为(2,0),半径为1,
∴A(1,0),B(3,0).
在Rt△OO1M中,
∵∠O1OM=30°,
∴OM=OO1•cos30°=2×
=
,
在Rt△MOF中,
∵OF=OM•cos30°=
×
=
,
∴MF=OM•sin30°=
×
=
,
∴点M坐标为(
,
).
(3)解:存在.
如图3,过点A作AP1⊥x轴,与OM交于点P1,此时Rt△AP1O∽Rt△MO1O,

过点A作AP2⊥OM,垂足为P2,过P2点作P2H⊥OA,垂足为H,此时Rt△AP2O∽Rt△O1MO.
∵∠AOP1=30°,
∴P1A=OA•tan∠AOP1=tan30°=
,
∴P1(1,
).
②过点A作AP2⊥OM,垂足为P2,过P2点作P2H⊥OA,垂足为H.
在Rt△OP2A中,
∵OA=1,∠AOP2=30°,
∴OP2=OA•cos30°=
,
在Rt△OP2H中,
∵OH=OP2•cos∠AOP2=
×
=
,P2H=OP2•sin∠AOP2=
×
=
,
∴P2(
,
).
∴符合条件的P点坐标有(1,
),(
,
).

∵M点为⊙O1切点,
∴MO1⊥OM,
在Rt△OMO1中,
∵MO1=1,OO1=2,
∴∠MOO1=30°,
∴∠MO1O=60°,
∵MO1=AO1,
∴△MAO1为等边三角形.
(2)解:如图2,过点M作MF⊥x轴,垂足为F.

∵⊙O1圆心O1的坐标为(2,0),半径为1,
∴A(1,0),B(3,0).
在Rt△OO1M中,
∵∠O1OM=30°,
∴OM=OO1•cos30°=2×
| ||
| 2 |
| 3 |
在Rt△MOF中,
∵OF=OM•cos30°=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
∴MF=OM•sin30°=
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴点M坐标为(
| 3 |
| 2 |
| ||
| 2 |
(3)解:存在.
如图3,过点A作AP1⊥x轴,与OM交于点P1,此时Rt△AP1O∽Rt△MO1O,

过点A作AP2⊥OM,垂足为P2,过P2点作P2H⊥OA,垂足为H,此时Rt△AP2O∽Rt△O1MO.
∵∠AOP1=30°,
∴P1A=OA•tan∠AOP1=tan30°=
| ||
| 3 |
∴P1(1,
| ||
| 3 |
②过点A作AP2⊥OM,垂足为P2,过P2点作P2H⊥OA,垂足为H.
在Rt△OP2A中,
∵OA=1,∠AOP2=30°,
∴OP2=OA•cos30°=
| ||
| 2 |
在Rt△OP2H中,
∵OH=OP2•cos∠AOP2=
| ||
| 2 |
| ||
| 2 |
| 3 |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
∴P2(
| 3 |
| 4 |
| ||
| 4 |
∴符合条件的P点坐标有(1,
| ||
| 3 |
| 3 |
| 4 |
| ||
| 4 |
点评:本题考查了圆切点的性质、含30°直角三角形的性质及利用三角函数解直角三角形的技巧,题目虽涉及圆、动点等问题类型,但其考查内容及技巧都是非常基础的,总体来说是一道非常值得练习的题目.

练习册系列答案
相关题目

 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).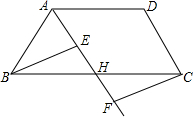 如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.
如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.