题目内容
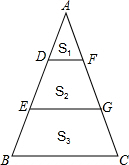如图，D、E是AB的三等分点，DF∥EG∥BC，图中三部分的面积分别为S1，S2，S3，则S1：S2：S3=（ ）| A、1：2：3 | B、1：2：4 | C、1：3：5 | D、2：3：4 |
分析：相似三角形对应边成比例，而面积比则为相似比的平方．
解答：解：∵D、E是AB的三等分点，且DF∥EG∥BC，∴△ADF∽△AEG，
∴
=
，
∴
=
，即S1：S2=1：3，
∴
=
=
=
，
同理
=
，
∴S1：S3=1：5，
∴S1：S2：S3=1：3：5，
故选C
∴
| DF |
| EG |
| 1 |
| 2 |
∴
| SADF |
| SAEG |
| 1 |
| 4 |
∴
| S1 |
| S2 |
| SADF |
| SAEG-S△ADF |
| 1 |
| 4-1 |
| 1 |
| 3 |
同理
| SADF |
| SABC |
| 1 |
| 9 |
∴S1：S3=1：5，
∴S1：S2：S3=1：3：5，
故选C
点评：熟练掌握平行线分线段成比例的性质及相似三角形的面积比与对应边之比的关系．
练习册系列答案
相关题目
23、如图所示，CD是AB的垂直平分线，若AC=1.6cm，BD=2.3cm，则四边形ABCD的周长是（ ）
25、已知，如图△ABC中，D是AB的中点，E是AC上一点，EF∥AB，DF∥BE．
如图，若点P是AB的黄金分割点，则线段AP，PB，AB满足关系式
如图所示，CD是AB的垂直平分线，若AC=10cm，BD=20cm，则四边形ACBD的周长为
如图，已知M是AB的中点，AC∥MD，AC=MD，试说明下面结论成立的理由：（1）△ACM≌△MDB；（2）CM=DB，CM∥DB．