题目内容
3. 如图,△ABC的三个顶点都在⊙O上,直径AD=6cm,∠DAC=2∠B,求AC的长.
如图,△ABC的三个顶点都在⊙O上,直径AD=6cm,∠DAC=2∠B,求AC的长.
分析 先连接OC,根据AO=AC=OC,判定△AOC是等边三角形,进而得到AC=AO=$\frac{1}{2}$AD=3cm.
解答  解:如图,连接OC,
解:如图,连接OC,
∵∠AOC=2∠B,∠DAC=2∠B,
∴∠AOC=∠DAC,
∴AO=AC,
又∵OA=OC,
∴△AOC是等边三角形,
∴AC=AO=$\frac{1}{2}$AD=3cm.
点评 本题主要考查了圆周角定理以及等边三角形的判定与性质的综合应用,解决问题的关键是作辅助线构造等边三角形.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
18.下列方程中,关于x的一元一次方程是( )
| A. | x2+2x=x2-1 | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | (x+1)2=2(x+1) |
8.下列图形中,是正方体的表面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
15.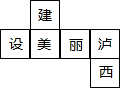 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A. | 美 | B. | 丽 | C. | 泸 | D. | 西 |
12.若点O是△ABC的外心,且∠BOC=70°,则∠BAC的度数为( )
| A. | 35° | B. | 110° | C. | 35°或145° | D. | 35°或140° |
13.已知a<-2,点(a-1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,则( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
 △ABC中,AB=AC,AD⊥BC,∠BAC=∠ACG=4∠EDC,CG=AD=4,$\frac{{{S_{△DEC}}}}{{{S_{△ACG}}}}$=$\frac{1}{4}$,BC=4$\sqrt{5}$.
△ABC中,AB=AC,AD⊥BC,∠BAC=∠ACG=4∠EDC,CG=AD=4,$\frac{{{S_{△DEC}}}}{{{S_{△ACG}}}}$=$\frac{1}{4}$,BC=4$\sqrt{5}$.