题目内容
6．
如图所示，△AEB≌△DFC，AE⊥CB，DF⊥BC，∠C=28°，则∠A的度数为62°．
分析 直接利用全等三角形的性质结合垂直的定义得出答案．
解答 解：∵△AEB≌△DFC，
∴∠C=∠B=28°，
∵AE⊥CB，DF⊥BC，
∴∠AEB=90°，
∴∠A=90°-28°=62°．
故答案为：62°．
点评 此题主要考查了全等三角形的性质以及垂直的定义，正确应用全等三角形的性质是解题关键．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
16．下列说法错误的是（ ）
| A． | 点（4，-1）与点（-4，1）关于原点对称 | |
| B． | 第一象限内的点的横坐标与纵坐标均为正数 | |
| C． | 点（2，3）和点（3，2）表示同一个点 | |
| D． | 坐标轴上的点的横坐标和纵坐标至少有一个为0 |
14．某商品的原价是每件x元，在销售时每件加价20元，再降价15%，则现在每件的售价是（ ）元．
| A． | 15%x+20 | B． | （1-15%）x+20 | C． | 15%（x+20） | D． | （1-15%）（x+20） |
11．下列运算，正确的是（ ）
| A． | $\sqrt{20}$=2$\sqrt{10}$ | B． | $\sqrt{4}$-$\sqrt{2}$=$\sqrt{2}$ | C． | $\sqrt{（-3）^{2}}$=-3 | D． | $\sqrt{3}$•$\sqrt{2}$=$\sqrt{6}$ |
18．如果ab=cd，则下列比例式中不一定成立的是（ ）
| A． | $\frac{a}{c}$=$\frac{d}{b}$ | B． | $\frac{a}{d}$=$\frac{c}{b}$ | C． | $\frac{a}{c}$=$\frac{b}{d}$ | D． | $\frac{c}{a}$=$\frac{b}{d}$ |
15．用配方法解一元二次方程x2+6x-3=0，原方程可变形为（ ）
| A． | （x+3）2=3 | B． | （x+3）2=6 | C． | （x+3）2=12 | D． | （x+3）2=9 |
4．
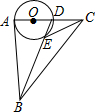如图，△ABC中，∠BAC=90°，AB=AC=2，D为AC上一动点，以AD为直径的⊙O交BD于E，则线段CE的最小值为（ ）
如图，△ABC中，∠BAC=90°，AB=AC=2，D为AC上一动点，以AD为直径的⊙O交BD于E，则线段CE的最小值为（ ）| A． | $\sqrt{5}$ | B． | $\sqrt{5}$+1 | C． | 2$\sqrt{5}$ | D． | $\sqrt{5}$-1 |