题目内容
已知菱形的一个内角是60°,较短的一条对角线的长为2cm,则较长的一条对角线的长为 cm.
考点:菱形的性质
专题:
分析:作出草图,根据菱形的对角线互相垂直平分求出可得AC⊥BD,OA=
AC,∠ABO=
∠ABC,再根据直角三角形30°角所对的直角边等于斜边的一半求出AB,利用勾股定理列式求出OB,然后根据BD=2OB计算即可得解.
| 1 |
| 2 |
| 1 |
| 2 |
解答: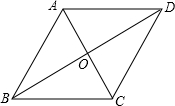 解:如图,在菱形ABCD中,AC⊥BD,OA=
解:如图,在菱形ABCD中,AC⊥BD,OA=
AC=
×2=1cm,∠ABO=
∠ABC=
×60°=30°,
在Rt△AOB中,AB=2OA=2×1=2,
由勾股定理得,OB=
=
=
cm,
∴BD=2OB=2×
=2
cm.
故答案为:2
.
 解:如图,在菱形ABCD中,AC⊥BD,OA=
解:如图,在菱形ABCD中,AC⊥BD,OA=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOB中,AB=2OA=2×1=2,
由勾股定理得,OB=
| AB2-OA2 |
| 22-12 |
| 3 |
∴BD=2OB=2×
| 3 |
| 3 |
故答案为:2
| 3 |
点评:本题考查了菱形的性质,主要利用了菱形的对角线互相垂直平分的性质,以及勾股定理的应用,熟记性质是解题的关键,作出图形更形象直观.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=
如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=| 12 |
| x |
(1)求证:线段AB为⊙P的直径;
(2)求△AOB的面积.
不透明的袋中装有3个分别标有数字1,2,3的小球,这些球除数字不同外,其它均相同.从中随机取出一个球,以该球上的数字作为十位数,再从袋中剩余2个球中随机取出一个球,以该球上的数字作为个位数,所得的两位数大于20的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
一元二次方程x(x-2)=0的解是( )
| A、0 | B、0或2 |
| C、2 | D、此方程无实数解 |
 如图,在△ABC和△DEF中,AB∥DE,可以推出∠
如图,在△ABC和△DEF中,AB∥DE,可以推出∠