题目内容
18．
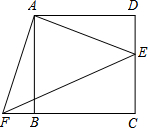如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转到△ABF的位置．（1）旋转中心是点A，旋转角度是90度；
（2）若四边形AECF的面积为25，DE=2，求EF的长．
分析 （1）根据性质的概念解答；
（2）根据旋转变换的性质求出FC、CE，根据勾股定理计算即可．
解答 解：（1）∵把△ADE顺时针旋转到△ABF的位置，
∴旋转中心是点A，旋转角为∠BAD=90°，
故答案为：A；90；
（2）由旋转变换的性质可知，△ADE≌△ABF，
∴正方形ABCD的面积=四边形AECF的面积=25，
∴BC=5，BF=DE=2，
∴FC=7，CE=3，
∴EF=$\sqrt{F{C}^{2}+C{E}^{2}}$=$\sqrt{58}$．
点评 本题考查的是旋转变换的性质、勾股定理的应用，掌握性质的概念、旋转变换的性质是解题的关键．
练习册系列答案
相关题目
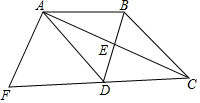如图，四边形ABCD中，BD垂直平分AC，垂足为点E，点F为四边形ABCD外一点，DA平分∠BDF，∠ADF=∠BAD，且AF⊥AC．