题目内容
4. 如图,四边形ABCD、AEFG是正方形,点E、G分别在AB、AD上,连接FC,过点E作EH∥FC,交BC于点H,若AB=4,AE=1,则BH=3.
如图,四边形ABCD、AEFG是正方形,点E、G分别在AB、AD上,连接FC,过点E作EH∥FC,交BC于点H,若AB=4,AE=1,则BH=3.
分析 求出BE的长,再根据两组对边分别平行的四边形是平行四边形求出四边形EFCH平行四边形,根据平行四边形的对边相等可得EF=CH,再根据正方形的性质可得AB=BC,AE=EF,然后求出BH=BE即可得解.
解答 解:∵AB=4,AE=1,
∴BE=AB-AE=4-1=3,
∵四边形ABCD,AEFG都是正方形,
∴AD∥EF∥BC,
又∵EH∥FC,
∴四边形EFCH平行四边形,
∴EF=CH,
∵四边形ABCD,AEFG都是正方形,
∴AB=BC,AE=EF,
∴AB-AE=BC-CH,
∴BE=BH=3.
故答案为:3.
点评 本题考查了正方形的性质,平行四边形的判定与性质,熟记性质并求出四边形EFCH平行四边形是解题的关键,也是本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.为调查聊城市某村开展“要致富,多读书”活动的效果,小红利用周末随机抽查了该村部分村民在一周内的阅读时间,并将结果绘制成如图两幅不完整的统计图,则本次调查的阅读时间的中位数和众数分别为( )
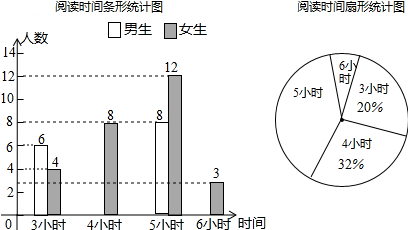

| A. | 4小时,5小时 | B. | 5小时,4小时 | C. | 4小时,4小时 | D. | 5小时,5小时 |
14.已知等腰三角形的周长等于20,那么底边长y与腰长x的函数解析式和定义域分别是( )
| A. | y=20-2x(0<x<20) | B. | y=20-2x(0<x<10) | C. | y=20-2x(5<x<10) | D. | y=$\frac{20-x}{2}$(5<x<10) |