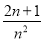题目内容
已知关于x的一元二次方程x2-(2k+1)x+k2+2k=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k,使得x1·x2-x12-x22≥0成立?若存在,请求出k的值;若不存在,请说明理由.
【答案】(1)当k≤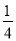 时,原方程有两个实数根(2)不存在实数k,使得x1·x2-x12-x22≥0成立
时,原方程有两个实数根(2)不存在实数k,使得x1·x2-x12-x22≥0成立
【解析】试题分析:(1)根据一元二次方程根的判别式列出不等式,解之即可;(2)本题利用韦达定理解决.
试题解析:
(1)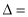
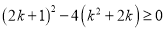 ,解得
,解得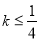
(2)由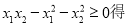
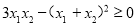 ,
,
由根与系数的关系可得: 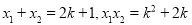
代入得: 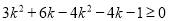 ,
,
化简得: 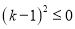 ,
,
得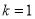 .
.
由于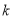 的取值范围为
的取值范围为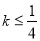 ,
,
故不存在k使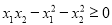 。
。
【题型】解答题
【结束】
13
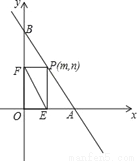
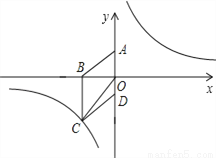
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且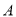 (0,3)、
(0,3)、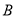 (﹣4,0).
(﹣4,0).
(1)求经过点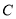 的反比例函数的解析式;
的反比例函数的解析式;
(2)设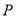 是(1)中所求函数图象上一点,以
是(1)中所求函数图象上一点,以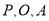 顶点的三角形的面积与△COD的面积相等.求点P的坐标.
顶点的三角形的面积与△COD的面积相等.求点P的坐标.
练习册系列答案
相关题目


 B.
B. C.
C. D.
D.

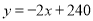 ;
;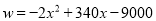 ,当
,当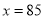 时,
时, 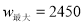 ;
;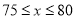 元时,在全部收回投资的基础上使第二个月的利润不低于1700元.
元时,在全部收回投资的基础上使第二个月的利润不低于1700元.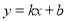 ,将(70,100),(75,90)代入上式得:
,将(70,100),(75,90)代入上式得: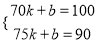 解得:
解得: 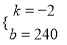 ,则
,则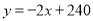 ;
;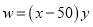
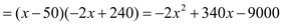 ,化为顶点式得,
,化为顶点式得, 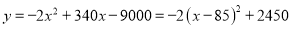 ,当
,当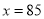 时,
时, 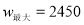
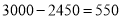 元的投资成本没有收回.则要想在全部收投资的基础上使第二个月的利润达到1700元, 即
元的投资成本没有收回.则要想在全部收投资的基础上使第二个月的利润达到1700元, 即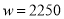 才可以,可得方程
才可以,可得方程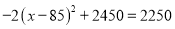 ,解得:
,解得: 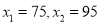 根据题意
根据题意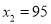 不合题意,应舍去.当
不合题意,应舍去.当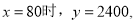 ,因为-2<0,则抛物线开口向下,当
,因为-2<0,则抛物线开口向下,当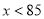 时,
时, 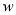 随
随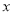 的增大而增大,当
的增大而增大,当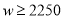 ,且销售单价不高于80时,
,且销售单价不高于80时, 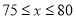
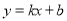 ,将(70,100),(75,90)代入上式得:
,将(70,100),(75,90)代入上式得: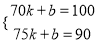 解得:
解得: 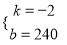 ,则
,则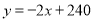 ,
,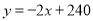
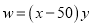
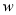 与
与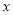 的关系式为
的关系式为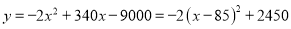
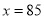 时,
时, 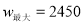
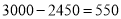 元的投资成本没有收回.
元的投资成本没有收回.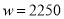 才可以,
才可以,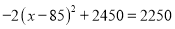 ,解得:
,解得: 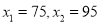
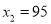 不合题意,应舍去.当
不合题意,应舍去.当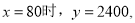 ,
,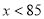 时,
时, 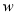 随
随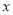 的增大而增大,
的增大而增大,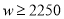 ,且销售单价不高于80时,
,且销售单价不高于80时, 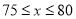
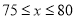 元时,在全部收回投资的基础上使第二个月的利润不低于1700元
元时,在全部收回投资的基础上使第二个月的利润不低于1700元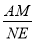 的值;
的值;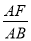 =k(k为大于
=k(k为大于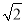 的常数),直接用含k的代数式表示
的常数),直接用含k的代数式表示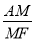 的值.
的值.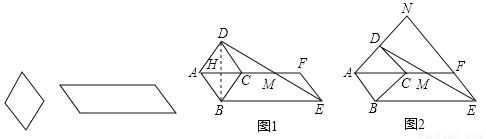
 是否需要挪走,并说明理由.
是否需要挪走,并说明理由.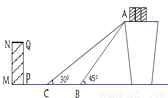
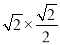 .
. 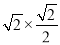 =4.
=4. 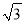 AD=4
AD=4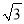 .
.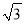 -4≈2.8.
-4≈2.8.
 的图象交于A(1,6),B(3,n)两点.
的图象交于A(1,6),B(3,n)两点.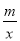 >0的解集;
>0的解集;
 ,
, 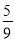 ,
, 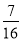 ,
, 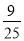 ,…,则第n个数为( )
,…,则第n个数为( )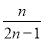 B.
B. 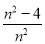 C.
C. 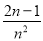 D.
D.