题目内容
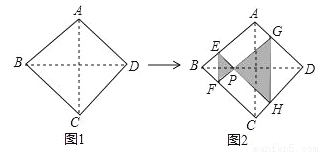
如图,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设BE=x(0<x<2),阴影部分面积为y,则y与x之间的函数图象为( )
A.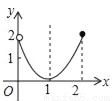 B.
B.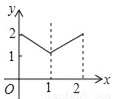 C.
C.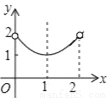 D.
D.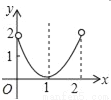
练习册系列答案
相关题目
题目内容
如图,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设BE=x(0<x<2),阴影部分面积为y,则y与x之间的函数图象为( )

A. B.
B. C.
C. D.
D.