题目内容
 如图,AB⊥BC于B,AD⊥DC于D,∠BAD=120°,在BC、CD上分别找一点M、N,当△AMN周长最小时,∠MAN的度数是
如图,AB⊥BC于B,AD⊥DC于D,∠BAD=120°,在BC、CD上分别找一点M、N,当△AMN周长最小时,∠MAN的度数是考点:轴对称-最短路线问题
专题:
分析:根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′=60°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″),然后根据三角形内角和即可得出答案.
解答:解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠DAB=120°,
∴∠HAA′=60°,
∴∠AA′M+∠A″=∠HAA′=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°,
∴∠MAN=60°
故答案为:60°.

∵∠DAB=120°,
∴∠HAA′=60°,
∴∠AA′M+∠A″=∠HAA′=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°,
∴∠MAN=60°
故答案为:60°.
点评:此题主要考查了平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M,N的位置是解题关键.

练习册系列答案
相关题目
下列各组数中互为相反数的是( )
| A、(-2)3与-23 | ||
B、2与
| ||
| C、-1与(-1)2 | ||
| D、2与|-2| |
下列说法错误的是( )
| A、两个互余的角都是锐角 |
| B、锐角的补角大于这个角本身 |
| C、互为补角的两个角不可能都是锐角 |
| D、锐角大于它的余角 |
若正三角形绕着它的中心旋转一定角度得到的图形与原来的图形完全重合,则它所转过的最小角度是( )
| A、60° | B、90° |
| C、120° | D、180° |
抛物线y=(1-m)x2-mx-m2+5m-6的图象过原点,则m的值为( )
| A、-6或1 | B、-6 |
| C、2 | D、2或3 |
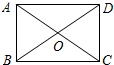 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的边长BC的长是( )
如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的边长BC的长是( )| A、2 | ||
| B、4 | ||
C、2
| ||
D、4
|
