Question

【题目】已知：是等腰直角三角形，，将绕点顺时针方向旋转得到，记旋转角为，当时，作，垂足为，与交于点

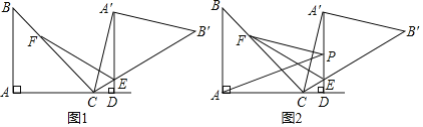
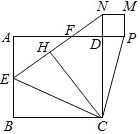
（1）如图1，当时，作的平分线交于点.

①写出旋转角的度数；②求证：；

（2）如图2，在（1）的条件下，设是直线上的一个动点，连接，，若，求线段的最小值.（结果保留根号）

Answer 1

【答案】（1）①旋转角为；②见解析；（2）的最小值为.

【解析】

（1）①解直角三角形求出即可解决问题.

②连接，设交于点.在时截取，连接.首先证明是等边三角形，再证明，即可解决问题.

（2）如图2中，连接，，，作交的延长线于.证明，推出，推出，关于对称，推出，推出，求出即可解决问题.

解：（1）①旋转角为．

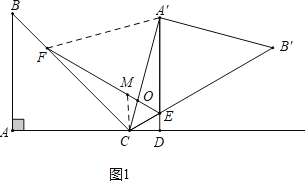
理由：如图1中，

∵，

∴，

∵，

∴，

∴，

∴旋转角为.

②证明：连接，设交于点.在时截取，连接.

∵，

∴，

∵平分，

∴，

∵，

∴，∵，

∴，

∴，

∴，

∵，

∴，

∴，

∴是等边三角形，

∴，

∵，，

∴是等边三角形，

，，

∵，

∴，

∴，

∴，

∴.

（2）解：如图2中，连接，，，作交的延长线于.

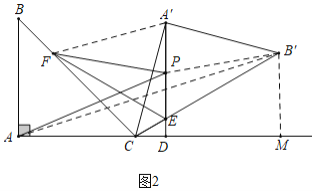
由②可知，，，，

∴，

∴，

∴，关于对称，

∴，

∴，

在中，，，

∴，，

∴.

∴的最小值为.