题目内容
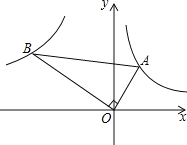
【题目】如图,已知第一象限内的点A在反比例函数y=![]() 上,第二象限的点B在反比例函数y=
上,第二象限的点B在反比例函数y=![]() 上,且OA⊥OB,cosA=
上,且OA⊥OB,cosA=![]() ,则k的值为______.
,则k的值为______.
【答案】-4
【解析】
作AC⊥x轴于点C,作BD⊥x轴于点D,易证△OBD∽△AOC,则面积的比等于相似比的平方,即tanA的平方,然后根据反比例函数中比例系数k的几何意义即可求解.
解:作AC⊥x轴于点C,作BD⊥x轴于点D.

则∠BDO=∠ACO=90°,
则∠BOD+∠OBD=90°,
∵OA⊥OB,cosA=![]() ,
,
∴∠BOD+∠AOC=90°,tanA=![]() ,
,
∴∠BOD=∠OAC,
∴△OBD∽△AOC,
∴![]() =(
=(![]() )2=(tanA)2=2,
)2=(tanA)2=2,
又∵S△AOC=![]() ×2=1,
×2=1,
∴S△OBD=2,
∴k=-4.
故答案为:-4.

练习册系列答案
相关题目
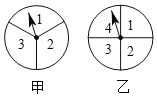
【题目】如图,甲、乙两个转盘分别被分成了![]() 等份与
等份与![]() 等份,每份内均标有数字.分别旋转这两个转盘,将转盘停止后指针所指区域内的两数相乘.
等份,每份内均标有数字.分别旋转这两个转盘,将转盘停止后指针所指区域内的两数相乘.
(1)请将所有可能出现的结果填入下表:
乙 积 甲 | 1 | 2 | 3 | 4 |
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
(2)积为![]() 的概率为 ;积为偶数的概率为 ;
的概率为 ;积为偶数的概率为 ;
(3)从![]() 这
这![]() 个整数中,随机选取
个整数中,随机选取![]() 个整数,该数不是(1)中所填数字的概率为 .
个整数,该数不是(1)中所填数字的概率为 .