题目内容
【题目】抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
![]() 求该抛物线所对应的函数解析式;
求该抛物线所对应的函数解析式;
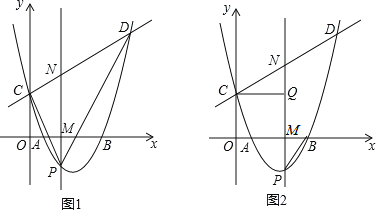
![]() 该抛物线与直线
该抛物线与直线![]() 相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线
相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线![]() 轴,分别与x轴和直线CD交于点M、N.
轴,分别与x轴和直线CD交于点M、N.
![]() 连结PC、PD,如图1,在点P运动过程中,
连结PC、PD,如图1,在点P运动过程中,![]() 的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
![]() 连结PB,过点C作
连结PB,过点C作![]() ,垂足为点Q,如图2,是否存在点P,使得
,垂足为点Q,如图2,是否存在点P,使得![]() 与
与![]() 相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.
相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.

【答案】(1)![]() ;(2)在点P运动过程中,
;(2)在点P运动过程中,![]() 的面积存在最大值,最大值为81;
的面积存在最大值,最大值为81;
存在点P,使得![]() 与
与![]() 相似,点P的坐标为
相似,点P的坐标为![]() 或
或![]() .
.
【解析】
(1)由A、B两点的坐标,利用待定系数法可求得抛物线解析式;
(2)①联立抛物线与直线CD的解析式成方程组,通过解方程组可求出点C、D的坐标,设点P的坐标为![]() ,则点N的坐标为
,则点N的坐标为![]() ,
,![]() ,根据三角形面积公式可得出
,根据三角形面积公式可得出![]() ,利用二次函数的性质即可解决最值问题;②利用相似三角形的性质可得出:若
,利用二次函数的性质即可解决最值问题;②利用相似三角形的性质可得出:若![]() 与
与![]() 相似,则有
相似,则有![]() 或
或![]() ,设点P的坐标为
,设点P的坐标为![]() ,则点N的坐标为
,则点N的坐标为![]() ,点M的坐标为
,点M的坐标为![]() ,点Q的坐标为
,点Q的坐标为![]() ,进而可得出
,进而可得出![]() ,
,![]() ,
,![]() ,
,![]() ,将其代入
,将其代入![]() 或
或![]() 中即可求出x的值,结合
中即可求出x的值,结合![]() 即可得出点P的坐标.
即可得出点P的坐标.
(1)∵抛物线![]() 经过点
经过点![]() 和点
和点![]() ,
,
![]() ,
,
解得![]() ,
,
![]() 该抛物线对应的函数解析式为
该抛物线对应的函数解析式为![]() ;
;
(2))①联立抛物线与直线CD的解析式成方程组,
得:![]() ,
,
解得:![]() ,
,![]() ,
,
与![]() 相似,点P的坐标为
相似,点P的坐标为![]() 或
或![]() .
.
设点P的坐标为![]() ,则点N的坐标为
,则点N的坐标为![]() ,
,
![]() ,
,
 .
.
![]() ,
,
![]() 当
当![]() 时,
时,![]() 取最大值,最大值为81,
取最大值,最大值为81,
![]() 在点P运动过程中,
在点P运动过程中,![]() 的面积存在最大值,最大值为81.
的面积存在最大值,最大值为81.
②∵![]() ,
,
![]() 若
若![]() 与
与![]() 相似,则有
相似,则有![]() 或
或![]() ,
,
设点P的坐标为![]() ,则点N的坐标为
,则点N的坐标为![]() ,点M的坐标为
,点M的坐标为![]() ,点Q的坐标为
,点Q的坐标为![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
当![]() 或时,有
或时,有![]() ,
,
解得:![]() ,
,![]() 舍去
舍去![]() ,
,
![]() 点P的坐标为
点P的坐标为![]() ;
;
当![]() 时,有
时,有![]() ,
,
解得:![]() ,
,![]() 舍去
舍去![]() ,
,
![]() 点P的坐标为
点P的坐标为![]() .
.
综上所述:存在点P,使得![]() 与
与![]() 相似,点P的坐标为
相似,点P的坐标为![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目





