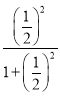Question

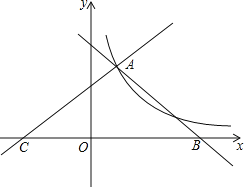
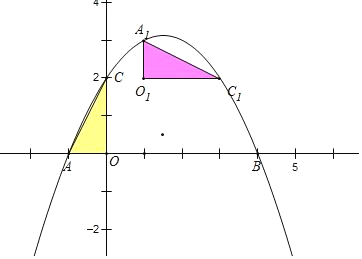
【题目】如图，已知抛物线经过点A（-1，0），B（4，0），C（0，2）三点，点D与点C关于x轴对称，点P是线段AB上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q，交直线BD于点M．

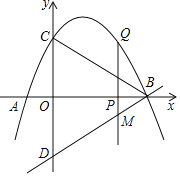
（1）求该抛物线所表示的二次函数的表达式；

（2）在点P运动过程中，是否存在点Q，使得△BQM是直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由；

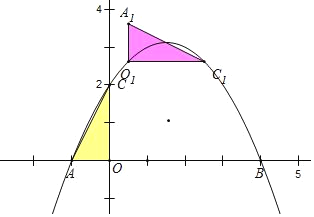
（3）连接AC，将△AOC绕平面内某点H顺时针旋转90°，得到△A1O1C1，点A、O、C的对应点分别是点A、O1、C1、若△A1O1C1的两个顶点恰好落在抛物线上，那么我们就称这样的点为“和谐点”，请直接写出“和谐点”的个数和点A1的横坐标．

Answer 1

【答案】（1）y=-+x+2；（2）存在，Q（3，2）或Q（-1，0）；（3）两个和谐点，A1的横坐标是1，.

【解析】

（1）把点A（1，0）、B（4，0）、C（0，3）三点的坐标代入函数解析式，利用待定系数法求解；

（2）分两种情况分别讨论，当∠QBM=90°或∠MQB=90°，即可求得Q点的坐标．

（3）（3）两个和谐点；AO=1，OC=2，设A1（x，y），则C1（x+2，y-1），O1（x，y-1），

①当A1、C1在抛物线上时，A1的横坐标是1；

当O1、C1在抛物线上时，A1的横坐标是2；

解：（1）设抛物线解析式为y=ax2+bx+c，

将点A（-1，0），B（4，0），C（0，2）代入解析式，

∴，

∴，

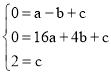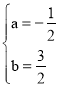∴y=-+x+2；

（2）∵点C与点D关于x轴对称，

∴D（0，-2）．

设直线BD的解析式为y=kx-2．

∵将（4，0）代入得：4k-2=0，

∴k=．

∴直线BD的解析式为y=x-2．

当P点与A点重合时，△BQM是直角三角形，此时Q（-1，0）；

当BQ⊥BD时，△BQM是直角三角形，

则直线BQ的直线解析式为y=-2x+8，

∴-2x+8=-+x+2，可求x=3或x=4（舍）

∴x=3；

∴Q（3，2）或Q（-1，0）；

（3）两个和谐点；

AO=1，OC=2，

设A1（x，y），则C1（x+2，y-1），O1（x，y-1），

①当A1、C1在抛物线上时，

∴，

∴，

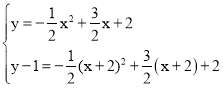∴A1的横坐标是1；

当O1、C1在抛物线上时，

，

∴，

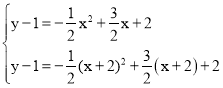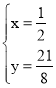∴A1的横坐标是；