��Ŀ����
13�� ��ͼ����ƽ��ֱ������ϵxOy�У�ÿ��С�����εı߳���Ϊ1���߶�AB��DE�Ķ˵�A��B��D��E����С�����εĶ����ϣ�
��ͼ����ƽ��ֱ������ϵxOy�У�ÿ��С�����εı߳���Ϊ1���߶�AB��DE�Ķ˵�A��B��D��E����С�����εĶ����ϣ���1��������ABΪһ�������Ϊ2��Rt��ABC������C������С�����εĶ����ϣ�
��2������һ����DEΪһ�ߣ�����45���ڽ������Ϊ$\frac{5}{2}$�ġ�DEF������F������С�����εĶ����ϣ�
��3������C�Ƶ�Q˳ʱ����ת90������F�غϣ���ֱ��д����Q�����꣮
���� ��1���ͣ�2���ֱ�ͼ�Σ���3����FC���д��ߣ���Q��5��0����
���  ��1��S��ABC=$\frac{1}{2}$��2��2=2��
��1��S��ABC=$\frac{1}{2}$��2��2=2��
��2��S��DEF=2��3-1��2-$\frac{1}{2}$��1��3=$\frac{5}{2}$��
��ED=EF����DFE=90�㣬
���FDE=45�㣻
��3���ɹ��ɶ����ã�FC=$\sqrt{{2}^{2}+{6}^{2}}$=$\sqrt{40}$��
CQ=$\sqrt{{2}^{2}+{4}^{2}}$=$\sqrt{20}$��FQ=$\sqrt{{2}^{2}+{4}^{2}}$=$\sqrt{40}$��
��FC2=CQ2+FQ2��CQ=FQ��
���FQC=90�㣬
���C�Ƶ�Q˳ʱ����ת90������F�غϣ�
���Q��5��0����
���� ���⿼������ͼ-��ת�任�����ڻ���ֵ����������Σ���������ĺ͡���������ij������ɵ�ͼ�ε�����Ƿ�������⣬��ȷ����һ�㣻ͬʱ���ݹ��ɶ����������ɵ��������Ƿ�Ϊֱ�������λ����ֱ�������Σ�

��ϰ��ϵ�д�
�����Ŀ
2��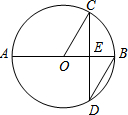 ��ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�E����CDB=30�㣬��O�İ뾶Ϊ5cm����Բ��O����CD�ľ���Ϊ��������
��ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�E����CDB=30�㣬��O�İ뾶Ϊ5cm����Բ��O����CD�ľ���Ϊ��������
 ��ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�E����CDB=30�㣬��O�İ뾶Ϊ5cm����Բ��O����CD�ľ���Ϊ��������
��ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�E����CDB=30�㣬��O�İ뾶Ϊ5cm����Բ��O����CD�ľ���Ϊ��������| A�� | $\frac{5}{2}$cm | B�� | 3cm | C�� | 3$\sqrt{3}$cm | D�� | 6cm |
5���������Ϊ6cm����Ϊ5cm�ij�����ֽƬ�۵�һ�Σ���ô�����ۺ۵ij��������ǣ�������
| A�� | 8cm | B�� | 5$\sqrt{2}$cm | C�� | 5.5cm | D�� | 1cm |
3�� ��ͼ����E��ֱ��AB�ϣ�ECƽ�֡�AED����DEB=100�㣬���ҪʹAB��CD�����C�Ķ���Ϊ��������
��ͼ����E��ֱ��AB�ϣ�ECƽ�֡�AED����DEB=100�㣬���ҪʹAB��CD�����C�Ķ���Ϊ��������
 ��ͼ����E��ֱ��AB�ϣ�ECƽ�֡�AED����DEB=100�㣬���ҪʹAB��CD�����C�Ķ���Ϊ��������
��ͼ����E��ֱ��AB�ϣ�ECƽ�֡�AED����DEB=100�㣬���ҪʹAB��CD�����C�Ķ���Ϊ��������| A�� | 30�� | B�� | 40�� | C�� | 50�� | D�� | 60�� |