题目内容
2.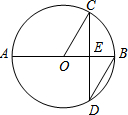 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为5cm,则圆心O到弦CD的距离为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为5cm,则圆心O到弦CD的距离为( )| A. | $\frac{5}{2}$cm | B. | 3cm | C. | 3$\sqrt{3}$cm | D. | 6cm |
分析 根据垂径定理知圆心O到弦CD的距离为OE;由圆周角定理知∠COB=2∠CDB=60°,已知半径OC的长,即可在Rt△OCE中求OE的长度.
解答  解:连接CB.
解:连接CB.
∵AB是⊙O的直径,弦CD⊥AB于点E,
∴圆心O到弦CD的距离为OE;
∵∠COB=2∠CDB(同弧所对的圆周角是所对的圆心角的一半),∠CDB=30°,
∴∠COB=60°;
在Rt△OCE中,
OC=5cm,OE=OC•cos∠COB,
∴OE=$\frac{5}{2}$cm.
故选A.
点评 本题考查了垂径定理、圆周角定理及解直角三角形的综合应用.解答这类题一些学生不会综合运用所学知识解答问题,不知从何处入手造成错解.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
12.在下列调查中,适宜采用全面调查的是( )
| A. | 了解浙江省中学生的视力情况 | |
| B. | 了解九(1)班学生校服的尺码情况 | |
| C. | 检测一批节能灯的使用寿命 | |
| D. | 调查湖州《阿奇讲事体》栏目的收视率 |
7. 如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )
如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )
 如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )
如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 8cm |
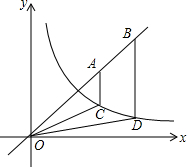 如图,点A,B为直线y=x上的两点,过A,B两点分别作y轴的平行线交双曲线y=$\frac{1}{x}$(x>0)于C,D两点,若2BD=5AC,则OC2-$\frac{4}{25}$OD2的值为$\frac{42}{25}$.
如图,点A,B为直线y=x上的两点,过A,B两点分别作y轴的平行线交双曲线y=$\frac{1}{x}$(x>0)于C,D两点,若2BD=5AC,则OC2-$\frac{4}{25}$OD2的值为$\frac{42}{25}$. 如图,在平面直角坐标系xOy中,每个小正方形的边长均为1,线段AB和DE的端点A、B、D、E均在小正方形的顶点上.
如图,在平面直角坐标系xOy中,每个小正方形的边长均为1,线段AB和DE的端点A、B、D、E均在小正方形的顶点上.