题目内容
16.如图1,在平面直角坐标系xOy中,点P在x轴的负半轴上,作⊙P交y轴于点A,B,交x轴于C,D两点,已知A(0,2),D(-1,0),且点A是弧DG的中点,连结DG,AG,DG与y轴交于点E.(1)求证:AE=DE;
(2)求P点的坐标及CG的长;
(3)如图2,点Q是⊙P上的一个动点,在x轴下方,连结AQ,交DG与点R,当△AGR是等腰三角形时,求GQ的值.(不需要过程,直接写出答案)
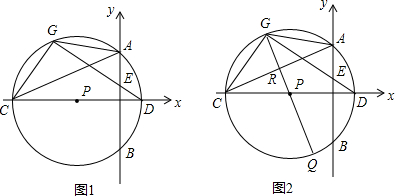
分析 (1)由A是DG$\widehat{DG}$的中点,得到$\widehat{AD}$=$\widehat{AG}$,AG=AD,因为CD是直径,AB⊥CD,得到AD=BD,∠BAD=∠ABD,∠BAD=∠ADE,所以AE=DE;
(2)由OA=2,OD=1,设半径为x,则OP=x-1,根据勾股定理得方程,求得P点的坐标及CG的长;
(3)有三种情况:①AR=GR时,GQ=AC=2;②AG=AR时,过C作CI⊥QG于I,连接CQ,由AG=AR得到∠AGR=∠ARG,∠AGD+∠QGD=∠ACG+∠CGQ,因为$\widehat{AG}$=$\widehat{AD}$,所以∠AGD=∠ACG,根据∠QGD+∠CGQ=90°,得到∠QGD=∠CGQ=45°,CQ=$\frac{1}{2}$CD=$\frac{5\sqrt{2}}{2}$,因为CI⊥GQ,所以IG=IC=$\frac{3\sqrt{2}}{2}$,RQ=$\sqrt{{CQ}^{2}{-CG}^{2}}=2\sqrt{2}$,GQ=$\frac{7\sqrt{2}}{2}$;
③当AG=RG时,作GH⊥AC于H,由∠GAC=∠GDC,∠GHC=∠DGC=90°,得到△AGH∽△DCG,$\frac{AG}{AH}$=$\frac{CD}{DG}$,AH=$\frac{4\sqrt{5}}{5}$,AR=$\frac{8\sqrt{5}}{5}$,CR=AC-AH-AR=$\frac{2\sqrt{5}}{5}$,根据∠GAR=∠Q,∠ARG=∠CRQ,RG=AG=$\sqrt{5}$,$\frac{RQ}{CR}$=$\frac{AR}{RG}$,得到RG=$\frac{16\sqrt{5}}{25}$,GQ=CR+RQ=$\frac{41\sqrt{5}}{25}$.
解答 证明:如图1(1)连结AD,BD,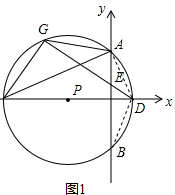
∵A是DG$\widehat{DG}$的中点,
∴$\widehat{AD}$=$\widehat{AG}$,
∴AG=AD,
∴∠AGD=∠ADG,
∵CD是直径,AB⊥CD,
∴AD=BD,
∴∠BAD=∠ABD,
∴∠BAD=∠ADE,
∴AE=DE;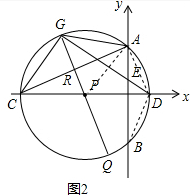
(2)如图2,由题意得:OA=2,OD=1
连结AP,设半径为x,则OP=x-1,
∴(x-1)2+22=x2,
解得:x=2.5,
∴P(-1.5,0),
∵AG=AD
∴AP⊥DG,DG=2DF,
∵S△ADP=$\frac{1}{2}$AP•DF=$\frac{1}{2}PD$•OA,PA=PD,
∴DF=OA=2
∴DG=4,∵CD=5,
∴CG=3;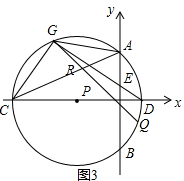
(3)如图3①AR=GR时,GQ=AC=2$\sqrt{5}$,
如图4②AG=AR时,GQ=$\frac{7\sqrt{2}}{2}$,
过C作CI⊥QG于I,连接CQ,
∵AG=AR∴∠AGR=∠ARG,
∴∠AGD+∠QGD=∠ACG+∠CGQ,
∵$\widehat{AG}$=$\widehat{AD}$,
∴∠AGD=∠ACG,
∴∠QGD=∠CGQ,
∵∠QGD+∠CGQ=90°,
∴∠QGD=∠CGQ=45°,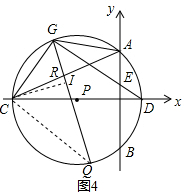
∴CQ=$\frac{1}{2}$CD=$\frac{5\sqrt{2}}{2}$,
∵CI⊥GQ,
∴IG=IC=$\frac{3\sqrt{2}}{2}$,
∴RQ=$\sqrt{{CQ}^{2}{-CG}^{2}}=2\sqrt{2}$,
∴GQ=$\frac{7\sqrt{2}}{2}$;
③如图5当AG=RG时,GQ=$\frac{41\sqrt{5}}{25}$,
作GH⊥AC于H,
∵∠GAC=∠GDC,∠GHC=∠DGC=90°,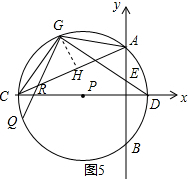
∴△AGH∽△DCG,
∴$\frac{AG}{AH}$=$\frac{CD}{DG}$,∴AH=$\frac{4\sqrt{5}}{5}$,
∴AR=$\frac{8\sqrt{5}}{5}$,
∴CR=AC-AH-AR=$\frac{2\sqrt{5}}{5}$,
∵∠GAR=∠Q,∠ARG=∠CRQ,RG=AG=$\sqrt{5}$,
∴$\frac{RQ}{CR}$=$\frac{AR}{RG}$,
∴RG=$\frac{16\sqrt{5}}{25}$,
∴GQ=CR+RQ=$\frac{41\sqrt{5}}{25}$,
综上所述:GQ的长度;2$\sqrt{5}$,$\frac{7\sqrt{2}}{2}$,$\frac{41\sqrt{5}}{25}$.
点评 本题主要考查了圆的性质,相似三角形的判定和性质,直角三角形的性质,勾股定理,等腰三角形的性质,平面直角坐标系中点的求法等知识点.

| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-3}\\{y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$ |
 已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2
已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2