Question

11．等腰△ABC中，AB=AC，过C点作CQ∥AB，P为BC上任意一点，连接AP．过P点作射线，使∠APQ=∠BAC，PQ交CQ于点Q；
（1）当∠BAC=90°时，求证：PA=PQ；                                                             
（2）当∠BAC=60°时，求证：PA=PQ；                                                           
（3）当∠BAC═α°时，（1）（2）的结论是否成立，并加以证明．

Answer 1

分析 （1）如图1中，作PE⊥AC于E，PF⊥CQ于F．只要证明△PAE≌△PQF即可．
（2）如图2中，作PE⊥AC于E，PF⊥CQ于F．证明方法类似．
（3）如图3中，结论不变．证明方法类似．

解答 证明：（1）如图1中，作PE⊥AC于E，PF⊥CQ于F．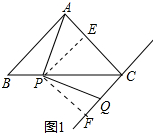

∵AB=AC，∠BAC=90°
∴∠B=∠ACB=45°，
∵AB∥CQ，
∴∠B=∠BCQ=45°，
∴∠PCA=∠PCQ，∵PE⊥AC，PF⊥CQ，
∴PE=PF，
∵∠EPF=∠ECF=90°，∠BAC=∠ECF=90°，
∴∠EPF=∠BAC=∠APQ=90°，
∴∠APE=∠QPF，
在△APE和△QPF中，
$\left\{\begin{array}{l}{∠APE=∠QPF}\\{PE=PF}\\{∠AEP=∠QFP}\end{array}\right.$，
∴△PAE≌△PQF，
∴PA=PQ．

（2）如图2中，作PE⊥AC于E，PF⊥CQ于F．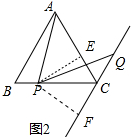

∵AB=AC=BC，
∴∠B=∠ACB=∠BAC=60°，
∵AB∥CQ，
∴∠B=∠BCQ=60°，
∴∠PCA=∠PCQ，∵PE⊥AC，PF⊥CQ，
∴PE=PF，
∵∠EPF+∠ECF=180°，∠ECF=120°
∴∠EPF=∠APQ=60°，
∴∠APE=∠QPF，
在△APE和△QPF中，
$\left\{\begin{array}{l}{∠APE=∠QPF}\\{PE=PF}\\{∠AEP=∠QFP}\end{array}\right.$，
∴△PAE≌△PQF，
∴PA=PQ．

（3）如图3中，结论不变．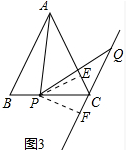

理由：作PE⊥AC于E，PF⊥CQ于F．
∵AB=AC，
∴∠B=∠ACB，
∵AB∥CQ，
∴∠B=∠BCQ，
∴∠PCA=∠PCQ，∵PE⊥AC，PF⊥CQ，
∴PE=PF，
∵∠EPF+∠ECF=180°，∠BAC+∠ECF=180°，
∴∠EPF=∠BAC=∠APQ，
∴∠APE=∠QPF，
在△APE和△QPF中，
$\left\{\begin{array}{l}{∠APE=∠QPF}\\{PE=PF}\\{∠AEP=∠QFP}\end{array}\right.$，
∴△PAE≌△PQF，
∴PA=PQ．

点评 本题考查三角形综合题、角平分线的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．