Question

16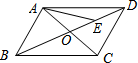．如图，在?ABCD中，AC与BD相交于点O，点E是OD 的中点，如$\overrightarrow{BA}$=$\overrightarrow{a}，\;\overrightarrow{BC}$=$\overrightarrow{b}$，那么$\overrightarrow{AE}$=$\frac{3}{4}$$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$．

Answer 1

分析 由四边形ABCD是平行四边形，根据平行四边形法则，可得$\overrightarrow{AD}$=$\overrightarrow{BC}$=$\overrightarrow{b}$，然后由三角形法则，求得$\overrightarrow{BD}$，又由点E是OD的中点，可求得$\overrightarrow{ED}$，再由三角形法则求得答案．

解答 解：∵四边形ABCD是平行四边形，
∴$\overrightarrow{AD}$=$\overrightarrow{BC}$=$\overrightarrow{b}$，OB=OD，
∴$\overrightarrow{BD}$=$\overrightarrow{BA}$+$\overrightarrow{AD}$=$\overrightarrow{a}$+$\overrightarrow{b}$，
∵点E是OD的中点，
∴$\overrightarrow{ED}$=$\frac{1}{4}$$\overrightarrow{BD}$=$\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$，
∴$\overrightarrow{AE}$=$\overrightarrow{ED}$-$\overrightarrow{AE}$=$\overrightarrow{b}$-（$\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$）=$\frac{3}{4}$$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$．
故答案为：$\frac{3}{4}\overrightarrow{b}-\frac{1}{4}\overrightarrow{a}$．

点评 此题考查了平面向量的知识以及平行四边形的性质．注意掌握三角形法则的应用．