题目内容
18.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2017次运动后,动点P的坐标是( )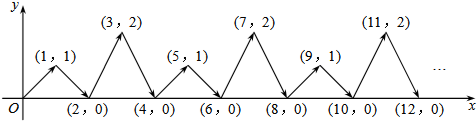
| A. | (2017,0) | B. | (2017,1) | C. | (2017,2) | D. | (2016,0) |
分析 根据已知提供的数据从横纵坐标分别分析得出横坐标为运动次数,纵坐标为1,0,2,0,每4次一轮这一规律,进而求出即可.
解答 解:根据动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),
第2次接着运动到点(2,0),第3次接着运动到点(3,2),
∴第4次运动到点(4,0),第5次接着运动到点(5,1),…,
∴横坐标为运动次数,经过第2017次运动后,动点P的横坐标为2017,
纵坐标为1,0,2,0,每4次一轮,
∴经过第2017次运动后,动点P的纵坐标为:2017÷4=504余1,
故纵坐标为四个数中第1个,即为1,
∴经过第2017次运动后,动点P的坐标是:(2017,1),
故选:B.
点评 此题主要考查了点的坐标规律,培养学生观察和归纳能力,从所给的数据和图形中寻求规律进行解题是解答本题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
6. 如图,现给出下列条件:①∠1=∠2,②∠B=∠5,③∠3=∠4,④∠5=∠D,⑤∠B+∠BCD=180°,其中能够得到AD∥BC的条件是①④.(填序号)
如图,现给出下列条件:①∠1=∠2,②∠B=∠5,③∠3=∠4,④∠5=∠D,⑤∠B+∠BCD=180°,其中能够得到AD∥BC的条件是①④.(填序号)
能够得到AB∥CD的条件是②③⑤.(填序号)
 如图,现给出下列条件:①∠1=∠2,②∠B=∠5,③∠3=∠4,④∠5=∠D,⑤∠B+∠BCD=180°,其中能够得到AD∥BC的条件是①④.(填序号)
如图,现给出下列条件:①∠1=∠2,②∠B=∠5,③∠3=∠4,④∠5=∠D,⑤∠B+∠BCD=180°,其中能够得到AD∥BC的条件是①④.(填序号)能够得到AB∥CD的条件是②③⑤.(填序号)
10.已知直线y=kx+b,其中k+b=-5,kb=6,那么直线经过象限为( )
| A. | 第二、四 | B. | 第二、三、四 | C. | 第一、三 | D. | 第一、二、三 |
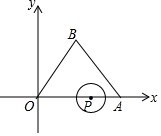 如图,等边三角形OAB的边长为8,点P沿O→A→B→O的方向运动,⊙P的半径是$\sqrt{3}$,⊙P运动一圈与△ABC的边相切几次,其中与边AB相切时,点P的坐标为(6,0),(3,3$\sqrt{3}$).
如图,等边三角形OAB的边长为8,点P沿O→A→B→O的方向运动,⊙P的半径是$\sqrt{3}$,⊙P运动一圈与△ABC的边相切几次,其中与边AB相切时,点P的坐标为(6,0),(3,3$\sqrt{3}$).