题目内容
3．解不等式组$\left\{\begin{array}{l}{3x-3＜2x}\\{\frac{x+3}{3}-\frac{1}{2}≥\frac{x-1}{6}}\end{array}\right.$，并求出它的整数解的和．分析 分别求出各不等式的解集，再求出其公共解集，在其公共解集内找出符合条件的x的整数解即可．
解答 解：$\left\{\begin{array}{l}{3x-3＜2x①}\\{\frac{x+3}{3}-\frac{1}{2}≥\frac{x-1}{6}②}\end{array}\right.$，
由①得，x＜3，
由②得，x≥-4，
此不等式组的解集为-4≤x＜3，
故它的整数解为：-4，-3，-2，-1，0，1，2．
它的整数解的和为-7．
点评 本题考查的是解一元一次不等式组及一元一次不等式组的整数解，能利用数形结合求不等式组的解集是解答此题的关键．
练习册系列答案
相关题目
13．
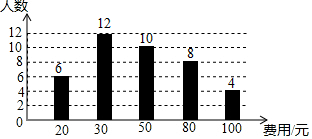某校开展“阅读季”活动，小明调查了班级里40名同学计划购书的花费情况，并将结果绘制成如图所示的条形统计图，根据图中相关信息，这次调查获取的样本数据的众数和中位数分别是（ ）
某校开展“阅读季”活动，小明调查了班级里40名同学计划购书的花费情况，并将结果绘制成如图所示的条形统计图，根据图中相关信息，这次调查获取的样本数据的众数和中位数分别是（ ）| A． | 12和10 | B． | 30和50 | C． | 10和12 | D． | 50和30． |
18．如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2017次运动后，动点P的坐标是（ ）
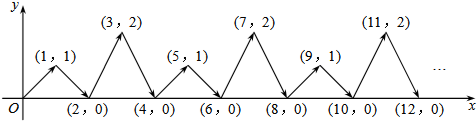
| A． | （2017，0） | B． | （2017，1） | C． | （2017，2） | D． | （2016，0） |
如图2×2的正方形网格放置在平面直角坐标系中，每个小正方形的顶点称为格点．每个小正方向的边长都是1，正方形ABCD的顶点都在格点上，若直线y=kx（k≠0）与正方形ABCD有公共点，则k不可能是（ ）