题目内容
2.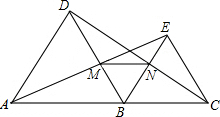 如图,B为线段AC上一动点(点B不与点A、C重合),在AC的同侧分别作等边△ABD和等边△BCE,AE与BD相交于点M,BE与CD相交于点N,连接MN.求证:(1)BM=BN;(2)MN∥AC.
如图,B为线段AC上一动点(点B不与点A、C重合),在AC的同侧分别作等边△ABD和等边△BCE,AE与BD相交于点M,BE与CD相交于点N,连接MN.求证:(1)BM=BN;(2)MN∥AC.
分析 (1)先根据等边三角形的性质得到BA=BD,BC=BE,∠ABD=∠CBE=60°,则∠DBE=60°,再利用“SAS”可判断△ABE≌△DBC,得到∠BAE=∠BDC,然后根据“ASA”可证明△BAM≌△BDN,则根据全等三角形的性质得到BM=BN;
(2)证明△BNM为等边三角形得到∠BMN=60°,则∠BMN=∠ABM,然后根据平行线的判定方法即可得到结论.
解答 证明:(1)∵△ABD和△BCE都是等边三角形,
∴BA=BD,BC=BE,∠ABD=∠CBE=60°,
∴∠DBE=60°,
在△ABE和△DBC中
$\left\{\begin{array}{l}{BA=BD}\\{∠ABE=∠DBC}\\{BE=BC}\end{array}\right.$,
∴△ABE≌△DBC,
∴∠BAE=∠BDC,
在△BAM和△BDN中
$\left\{\begin{array}{l}{∠BAM=∠BDN}\\{BA=BD}\\{∠ABM=∠DBN}\end{array}\right.$,
∴△BAM≌△BDN,
∴BM=BN;
(2)∵BM=BN,∠MBN=60°,
∴△BNM为等边三角形,
∴∠BMN=60°,
∴∠BMN=∠ABM,
∴MN∥AC.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.也考查了等边三角形的判定与性质.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
14.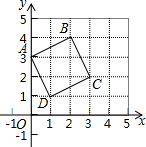 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD沿x轴翻折一次,再沿轴翻折一次,然后向右平移1个单位记作:图形的一次完整变化,图形经历100次这样完整的变化后,点B到达的位置坐标为( )
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD沿x轴翻折一次,再沿轴翻折一次,然后向右平移1个单位记作:图形的一次完整变化,图形经历100次这样完整的变化后,点B到达的位置坐标为( )
 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD沿x轴翻折一次,再沿轴翻折一次,然后向右平移1个单位记作:图形的一次完整变化,图形经历100次这样完整的变化后,点B到达的位置坐标为( )
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD沿x轴翻折一次,再沿轴翻折一次,然后向右平移1个单位记作:图形的一次完整变化,图形经历100次这样完整的变化后,点B到达的位置坐标为( )| A. | (-1,-4) | B. | (2,4) | C. | (-1,-4) | D. | (1,4) |
11.为了保护生态平衡,绿化环境,国家大力鼓励“退耕还林、还草”,其补偿政策如表(一);某农户承包了一片山坡地种树种草,所得到国家的补偿如表(二).问:该农户种树、种草各多少亩?
表(一)种树、种草每亩每年补粮补钱情况表
表(二)该农户收到乡政府下发的当种树种草亩数及年补偿通知单
表(一)种树、种草每亩每年补粮补钱情况表
| 种树 | 种草 | |
| 补粮 | 150千克 | 100千克 |
| 补钱 | 200元 | 150元 |
| 种树、种草 | 补粮 | 补钱 |
| 30亩 | 4000千克 | 5500元 |
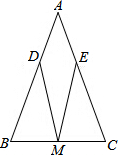 如图,已知:△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE,
如图,已知:△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE,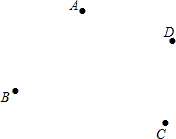 如图,已知四点A、B、C、D,按要求作图
如图,已知四点A、B、C、D,按要求作图