题目内容
已知实数a、b满足（a-3）2+|2a-3b+7|=0，求代数式a2-b2的值．
考点：解二元一次方程组,非负数的性质：绝对值,非负数的性质：偶次方
专题：
分析：根据偶次方和绝对值的非负性得出方程a-3=0，2a-3b+7=0，求出组成的方程组的解即可．
解答：解：∵根据偶次方和绝对值的非负性
∴根据原式（a-3）2+|2a-3b+7|=0，
可得a-3=0，2a-3b+7=0，
∴a=3，b=
，
∴a2-b2=32-（
）2=-
．
故答案为：-
．
∴根据原式（a-3）2+|2a-3b+7|=0，
可得a-3=0，2a-3b+7=0，
∴a=3，b=
| 13 |
| 3 |
∴a2-b2=32-（
| 13 |
| 3 |
| 88 |
| 9 |
故答案为：-
| 88 |
| 9 |
点评：本题考查了解二元一次方程组，偶次方，绝对值的非负性的应用，解此题的关键是能根据题意得出方程组．
练习册系列答案
口算能手系列答案
相关题目
如图在平行四边形ABCD中，AC交BD于点O，AE⊥BD，CF⊥BD，垂足分别为E、F，求证：四边形AECF为平行四边形．
如图所示，OA⊥OB，OC⊥OD，OE为∠BOD的平分线，∠BOE=17°．求∠AOC的度数．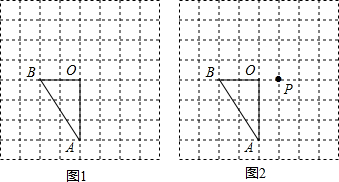
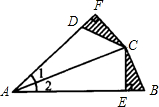如图，在△ABC中，CE⊥AB于E，在△ABC外作∠CAD=∠CAB，过C作CF⊥AD，交AD的延长线于F，且∠FDC=∠B，求证：BE=DF．