点O是△ABC的外心.若∠BCO=40°.则∠BAC的度数为( )A．50°B．100°C．50°或130°D．50°或100° 题目和参考答案——青夏教育精英家教网—

题目内容

7．点O是△ABC的外心，若∠BCO=40°，则∠BAC的度数为（　　）

A．

50°

B．

100°

C．

50°或130°

D．

50°或100°

分析根据等腰三角形的性质求出∠BOC的度数，分△ABC是锐角三角形和△ABC是钝角三角形两种情况，根据圆周角定理计算即可．

解答解：∵OB=OC，∠BCO=40°，
∴∠BOC=100°，
当△ABC是锐角三角形时，∠BAC=50°，
当△ABC是钝角三角形时，∠BAC=130°．
故选：C．

点评本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了等腰三角形的性质．

练习册系列答案

本土教辅名校学案黄冈期末全程特训卷系列答案

18．分解因式：9m³-mn²=m（3m+n）（3m-n）．

15．

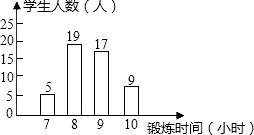阳光体育运动，要求学生每一天锻炼一小时，如图是依据某班40名同学一周的体育锻炼时间绘制的条形统计图，那么关于该班50名同学一周参加体育锻炼时间的中位数为9小时．

2．

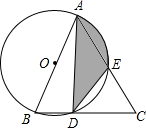如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交于点D、E，连接DE、AD．
（1）求证：BC=2DE；
（2）若⊙O的半径为2，∠CDE=45°，求阴影部分的面积．

12．已知分式M=$\frac{x}{x-3}$+$\frac{y}{y-3}$．
（1）若x=6且分式M的值等于4，求y的值；
（2）若y=4，当x取哪些整数时，M的值是整数？
（3）若x、y均为正整数，写出使M的值等于2的所有x、y的值．

19．

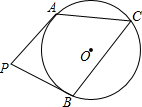如图，PA，PB分别与⊙O相切于A，B两点，sin∠C=$\frac{4}{5}$，PA=$\frac{20}{3}$，则⊙O的面积为（　　）

16．若点P的坐标是（x，y），且满足x²+$\sqrt{y}$=0，则点P在（　　）

10．三边长分别为9，12，15的三角形的面积为54．

试题分类