题目内容
重庆一中后勤部门每年都要更新一定数量的书桌和椅子.已知2012年采购的书桌价格为120元/张,椅子价格为40元/张,总支出费用34000元;2013年采购的书桌价格上涨为130元/张,椅子价格保持不变,且采购的书桌和椅子的数量与2012年分别相同,总支出费用比2012年多2000元.
(1)求2012年采购的书桌和椅子分别是多少张?
(2)与2012年相比,2014年书桌的价格上涨了a%(其中0<a<50),椅子的价格上涨了10%,但采购的书桌的数量减少了
a%,椅子的数量减少了50张,且2014年学校桌子和椅子的总支出费用为34720元,求a的值.
(1)求2012年采购的书桌和椅子分别是多少张?
(2)与2012年相比,2014年书桌的价格上涨了a%(其中0<a<50),椅子的价格上涨了10%,但采购的书桌的数量减少了
| 1 |
| 2 |
考点:一元二次方程的应用,二元一次方程组的应用
专题:
分析:(1)可设2012年采购的书桌为x张,椅子为y张,根据等量关系:2012年采购的书桌价格为120元/张,椅子价格为40元/张,总支出费用34000元;2013年采购的书桌价格上涨为130元/张,椅子价格保持不变,且采购的书桌和椅子的数量与2012年分别相同,总支出费用比2012年多2000元;列出方程组求解即可;
(2)根据等量关系:2014年学校桌子和椅子的总支出费用为34720元,列出关于a的方程求解即可.
(2)根据等量关系:2014年学校桌子和椅子的总支出费用为34720元,列出关于a的方程求解即可.
解答:解:(1)设2012年采购的书桌为x张,椅子为y张.依题意有
,
解得
.
答:2012年采购的书桌是200张,椅子分别是250张.
(2)依题意有120(1+a%)200(1-
a%)+40(1+10%)(250-50)=34720,
令a%=t,则原方程可化简为:25t2-25t+4=0,
解得a1=0.2,a2=0.8(舍去).
答:2013年采购书桌和椅子分别是200张和250张.
|
解得
|
答:2012年采购的书桌是200张,椅子分别是250张.
(2)依题意有120(1+a%)200(1-
| 1 |
| 2 |
令a%=t,则原方程可化简为:25t2-25t+4=0,
解得a1=0.2,a2=0.8(舍去).
答:2013年采购书桌和椅子分别是200张和250张.
点评:考查了二元一次方程组的应用和一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程(组),再求解.

练习册系列答案
相关题目
 如图,数轴上的点P表示的实数可能是( )
如图,数轴上的点P表示的实数可能是( )A、-
| ||
B、-2
| ||
C、-
| ||
D、2
|
能清楚的看出每个项目的具体数量的统计图是( )
| A、扇形统计图 |
| B、折线统计图 |
| C、条形统计图 |
| D、以上三种均可 |
抛物线y=x2+3x-4与x轴交点的个数为( )
| A、1个 | B、2个 | C、0个 | D、3个 |
 已知抛物线y=x2+bx+c的图象如图所示,则一元二次方程x2+bx+c=0的解是
已知抛物线y=x2+bx+c的图象如图所示,则一元二次方程x2+bx+c=0的解是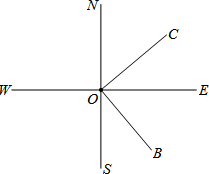 如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.
如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余. 已知:点A、C分别是∠B的两条边上的点,点D、E分别是直线BA、BC上的点,直线AE、CD相交于点P点,D、E分别在线段BA、BC上.若∠B=60°,且AD=BE,BD=CE,求∠APD的度数.
已知:点A、C分别是∠B的两条边上的点,点D、E分别是直线BA、BC上的点,直线AE、CD相交于点P点,D、E分别在线段BA、BC上.若∠B=60°,且AD=BE,BD=CE,求∠APD的度数. 如图,几块大小不等的正方形纸片无重叠地铺满了一块长方形.已知正方形纸片A的边长为7,求最小的正方形纸片的边长.
如图,几块大小不等的正方形纸片无重叠地铺满了一块长方形.已知正方形纸片A的边长为7,求最小的正方形纸片的边长.