Question

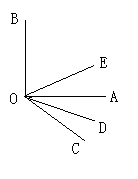
如图，OD是∠AOC的平分线，OE是∠BOC的平分线。
（1）如果∠AOC=48° ，∠BOC=42° ，求∠DOE的度数。
（2）如图∠AOB的大小不变，与（1）相同，而射线OC在∠AOB的内部绕点O旋转，∠DOE的大小是否发生变化？若不变，请求出其度数。
（3）如果∠AOB的大小仍不变，而射线OC在∠AOB的外部绕点O旋转（∠AOC不大于90° ），OD是
∠AOC的平分线，OE是∠BOC的平分线，请画出相应的图形，此时∠DOE的大小是否发生变化？并说明理由。

Answer 1

解：（1）因为OD、OE分别是∠AOC、∠BOC的平分线，
∠AOC=48°，∠BOC=42°，
所以∠D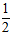OC= ∠AOC= 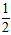×48°=24°，
∠COE= 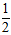∠BOC= 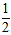×42°=21°．
所以∠DOE=∠DOC+∠EOC=24°+21°=45°
（2）因为OD 、OE 分别是∠AOC 、∠BOC 的平分线，
所以∠DOC=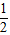∠AOC ，∠COE=∠BOC ．
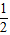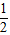所以∠DOE= ∠DOC+ ∠EOC=∠AOC+∠BOC=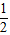（∠AOC+ ∠BOC 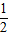）=∠AOB ．
因为∠AOB= ∠AOC+ ∠BOC=48 °+42 °=90 °，
所以∠DOE=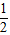 ∠AOB=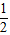 ×90 °=45 °．
故∠DOE 的大小不变，仍为45 °
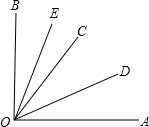
（3）∠DOE的大小不变，仍为45。
理由：如图，因为OD、OE分别是∠AOC、∠BOC的平分线
所以∠DOC=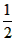∠AOC ，∠COE=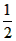∠BOC
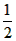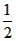所以∠DOE=∠EOC-∠DOC =∠BOC-∠AOC =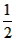（∠BOC-∠AOC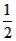） =∠AOB
因为∠AOB=90°
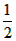所以∠DOE=∠AOB=×90°=45°
故∠DOE的大小不变，仍为45°。