题目内容
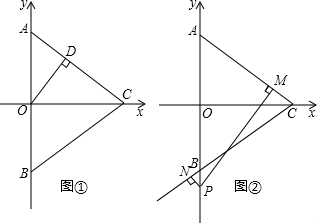
已知抛物线y=-x2+4x-3交x轴于A,B两点(点A在点B的左边),交y轴于C点.
(1)求直线BC的解析式;
(2)已知点M在线段BC上运动(不与点B,C重合),将OM绕点O逆时针转90°到OM′的位置,当点M′落在抛物线上时,求点M的坐标;
(3)将抛物线向左平移3个单位,得到抛物线y0,已知点P(2a,y1)、M(4a,y2)、N(7a,y3)都在抛物线y0上,是否存在含有y1,y2,y3,且与a无关的等式?如果存在,试给出一个,并加以证明;如果不存在,请说明理由.
(1)求直线BC的解析式;
(2)已知点M在线段BC上运动(不与点B,C重合),将OM绕点O逆时针转90°到OM′的位置,当点M′落在抛物线上时,求点M的坐标;
(3)将抛物线向左平移3个单位,得到抛物线y0,已知点P(2a,y1)、M(4a,y2)、N(7a,y3)都在抛物线y0上,是否存在含有y1,y2,y3,且与a无关的等式?如果存在,试给出一个,并加以证明;如果不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)当x=0时,求出y的值就可以求出C的坐标,当y=0时求出x得值,求出B的坐标,设BC的解析式为y=kx+b,由待定系数法求出结论即可;
(2)过点M作ME⊥y轴于E,M′F⊥x轴于F,就可以得出△EOM≌△FOM′,设出M、M′的坐标,表示出ME与′F的值,根据全等三角形的性质建立方程求出其值即可;
(3)根据解析式求出平移后的解析式,分别表示出有y1,y2,y3的值,再根据数量关系就可以求出结论.
(2)过点M作ME⊥y轴于E,M′F⊥x轴于F,就可以得出△EOM≌△FOM′,设出M、M′的坐标,表示出ME与′F的值,根据全等三角形的性质建立方程求出其值即可;
(3)根据解析式求出平移后的解析式,分别表示出有y1,y2,y3的值,再根据数量关系就可以求出结论.
解答:解:(1)当x=0时,y=-3,
∴C(0,-3).
当y=0时,-x2+4x-3=0,
解得:x1=1,x2=3.
∵点A在点B的左边,
∴A(1,0),B(3,0).
设直线BC的解析式为y=kx+b,由题意,得
,
解得:
,
∴直线BC的解析式为:y=x-3;
 (2)过点M作ME⊥y轴于E,M′F⊥x轴于F,
(2)过点M作ME⊥y轴于E,M′F⊥x轴于F,
∴∠OEM=∠OFM′=90°.
∵∠MOE+∠MOB=90°,∠M′OF+∠MOB=90°,
∴∠MOE=∠M′OF.
在△EOM和△FOM′中,
,
∴△EOM≌△FOM′(AAS),
∴OE=OF,ME=M′F.
设M(m,m-3),
∴OE=3-m,ME=m,
∴OF=3-m,
∴M′(3-m,-m2+2m),
∴M′F=-m2+2m.
∴m=-m2+2m,
解得:m1=0舍去,m2=1,
∴M(1,-2).
答:M(1,-2);
(3)∵y=-x2+4x-3,
∴y=-(x-2)2+1,
∴抛物线向左平移3个单位为:y0=-(x+1)2+1,
∴y0=-x2-2x.
∵P(2a,y1)、M(4a,y2)、N(7a,y3)都在抛物线y0上,
∴y1=-4a2-4a,y2=-16a2-8a,y3=-49a2-14a.
∴-42y1=168a2+168a,35y2=-560a2-280a,8y3=-392a2-112a.
∴-42y1+35y2=168a2+168a-560a2-280a=-392a2-112a.
∴8y3=-42y1+35y2.
∴C(0,-3).
当y=0时,-x2+4x-3=0,
解得:x1=1,x2=3.
∵点A在点B的左边,
∴A(1,0),B(3,0).
设直线BC的解析式为y=kx+b,由题意,得
|
解得:
|
∴直线BC的解析式为:y=x-3;
 (2)过点M作ME⊥y轴于E,M′F⊥x轴于F,
(2)过点M作ME⊥y轴于E,M′F⊥x轴于F,∴∠OEM=∠OFM′=90°.
∵∠MOE+∠MOB=90°,∠M′OF+∠MOB=90°,
∴∠MOE=∠M′OF.
在△EOM和△FOM′中,
|
∴△EOM≌△FOM′(AAS),
∴OE=OF,ME=M′F.
设M(m,m-3),
∴OE=3-m,ME=m,
∴OF=3-m,
∴M′(3-m,-m2+2m),
∴M′F=-m2+2m.
∴m=-m2+2m,
解得:m1=0舍去,m2=1,
∴M(1,-2).
答:M(1,-2);
(3)∵y=-x2+4x-3,
∴y=-(x-2)2+1,
∴抛物线向左平移3个单位为:y0=-(x+1)2+1,
∴y0=-x2-2x.
∵P(2a,y1)、M(4a,y2)、N(7a,y3)都在抛物线y0上,
∴y1=-4a2-4a,y2=-16a2-8a,y3=-49a2-14a.
∴-42y1=168a2+168a,35y2=-560a2-280a,8y3=-392a2-112a.
∴-42y1+35y2=168a2+168a-560a2-280a=-392a2-112a.
∴8y3=-42y1+35y2.
点评:本题考查了二次函数的解析式的运用,待定系数法求一次函数的解析式的运用,旋转的旋转的运用,全等三角形的判定及性质的运用,一元二次方程的解法的运用,解答时由二次函数的性质求解是关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知二次函数y=-x2+4x-3,则下列说法正确的是( )
| A、函数有最大值1 |
| B、函数有最小值1 |
| C、函数有最大值-1 |
| D、函数有最小值-1 |