题目内容
2. 如图,已知四边形ABCD的对角线AC、BD交于点F,点E是BD上一点,且∠BCA=∠ADE,∠CAD=∠BAE.
如图,已知四边形ABCD的对角线AC、BD交于点F,点E是BD上一点,且∠BCA=∠ADE,∠CAD=∠BAE.(1)求证:△ABC∽△AED;
(2)求证:BE•AC=CD•AB.
分析 (1)根据已知条件和角的和差得到∠BAC=∠DAE,由于∠ACB=∠ADE,即可得到结论;
(2)根据相似三角形的性质得到$\frac{AB}{AC}=\frac{AE}{AD}$,由∠BAE=∠CAD,推出△ABE∽△ACD,由相似三角形的性质即可得到结论.
解答 证明:(1)∵∠BAE=∠DAC,∠BAC=∠BAE-∠CAE,∠DAE=∠DAC-∠CAE,
∴∠BAC=∠DAE,
∵∠ACB=∠ADE,
∴△ABC∽△AED;
(2)∵△ABC∽△AED,
∴$\frac{AB}{AC}=\frac{AE}{AD}$,
∵∠BAE=∠CAD,
∴△ABE∽△ACD,
∴$\frac{BE}{CD}=\frac{AB}{AC}$,
即:BE•AC=CD•AB.
点评 此题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列各式中,结果为正数的是( )
| A. | -|-2| | B. | -(-2) | C. | -22 | D. | (-2)×2 |
10.如果两个相似三角形的周长比为1:4,那么这两个三角形的相似比为( )
| A. | 1:2 | B. | 1:4 | C. | 1:8 | D. | 1:16 |
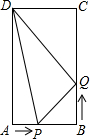 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向终点B以1cm/s的速度移动;同时,点Q从点B沿边BC向终点C以2cm/s的速度移动.设移动时间为t秒,解答下列问题:
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向终点B以1cm/s的速度移动;同时,点Q从点B沿边BC向终点C以2cm/s的速度移动.设移动时间为t秒,解答下列问题: